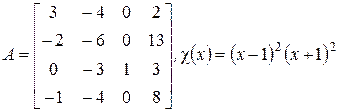 .
.
Следовательно, жорданова нормальная форма 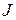 матрицы
матрицы 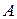 состоит из клеток Жордана с числами I и –I на диагонали. Количество всех клеток с числом I на диагонали равно
состоит из клеток Жордана с числами I и –I на диагонали. Количество всех клеток с числом I на диагонали равно 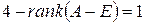 . Количество всех клеток с числом –I на диагонали равно
. Количество всех клеток с числом –I на диагонали равно 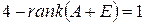 .
.
Значит,
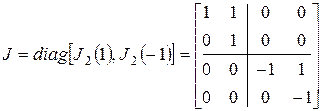 .
.
Пример 2. Найти жорданову нормальную форму 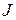 матрицы
матрицы
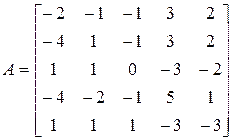 .
. 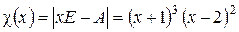 .
.
Следовательно, на диагонали 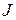 стоят клетки Жордана с числами -I и 2. Количество всех клеток с числом -I на диагонали равно
стоят клетки Жордана с числами -I и 2. Количество всех клеток с числом -I на диагонали равно 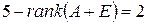 . Количество всех клеток с числом 2 на диагонали равно
. Количество всех клеток с числом 2 на диагонали равно 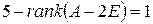 . Так как число
. Так как число 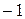 является 3-кратным корнем характеристического многочлена, то на диагонали матрицы
является 3-кратным корнем характеристического многочлена, то на диагонали матрицы 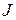 стоит одна клетка Жордана порядка
стоит одна клетка Жордана порядка 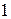 и одна клетка Жордана порядка 2 с числом
и одна клетка Жордана порядка 2 с числом 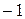 на диагонали. Значит,
на диагонали. Значит,
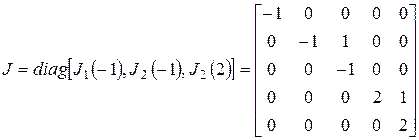 .
.
Пример 3. Найти жорданову нормальную форму 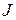 матрицы
матрицы
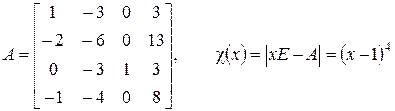 .
.
Следовательно, по теореме Гамильтона-Кэли 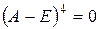 , т.е. линейный оператор с матрицей
, т.е. линейный оператор с матрицей 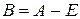 является нильпотентным.
является нильпотентным.
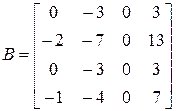 .
.
Жорданова нормальная форма матрицы 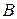 найдена в § 2. Она равна
найдена в § 2. Она равна
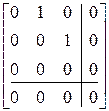 .
.
Значит, 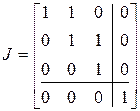 .
.
Пусть 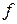 — линейный оператор
— линейный оператор 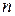 -мерного линейного пространства,
-мерного линейного пространства, 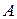 — его матрица в некотором базисе. Укажем сейчас способ построения канонического базиса относительно
— его матрица в некотором базисе. Укажем сейчас способ построения канонического базиса относительно 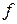 , зная жорданову нормальную форму
, зная жорданову нормальную форму 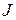 матрицы
матрицы 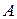 . Для этого достаточно найти матрицу
. Для этого достаточно найти матрицу 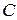 перехода от данного базиса к искомому каноническому. Как известно, тогда
перехода от данного базиса к искомому каноническому. Как известно, тогда
|
|
|
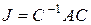 (I)
(I)
Матрица 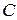 , удовлетворяющая равенству (I), может быть найдена следующим путем. Умножим обе части равенства (I) слева на
, удовлетворяющая равенству (I), может быть найдена следующим путем. Умножим обе части равенства (I) слева на 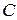 и перенесем все члены полученного равенства в левую часть. Получим равенство
и перенесем все члены полученного равенства в левую часть. Получим равенство
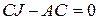 , (2)
, (2)
которое можно рассматривать как однородную систему линейных уравнений, в которой неизвестными являются элементы матрицы 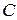 . Любое решение такой системы, удовлетворяющее дополнительному условию
. Любое решение такой системы, удовлетворяющее дополнительному условию
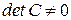
дает нужную матрицу 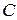 . Такое решение существует ввиду подобия
. Такое решение существует ввиду подобия 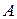 и
и 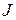 .
.
Упражнение. Известно, что матрицы с элементами из бесконечного поля 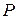 подобны над расширением этого поля. Доказать, что они подобны над полем
подобны над расширением этого поля. Доказать, что они подобны над полем 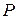 .
.

§ 5. Обобщенная жорданова нормальная форма.
Пусть 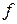 — линейный оператор действительного
— линейный оператор действительного 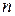 -мерного линейного пространства. Так как характеристический полином оператора
-мерного линейного пространства. Так как характеристический полином оператора 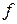 может иметь недействительные корни, то канонический базис относительно
может иметь недействительные корни, то канонический базис относительно 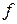 , вообще говоря, не существует. Тем не менее в действительном пространстве можно найти некоторую естественную замену жордановой нормальной формы матрицы оператора
, вообще говоря, не существует. Тем не менее в действительном пространстве можно найти некоторую естественную замену жордановой нормальной формы матрицы оператора 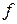 .
.
Пусть 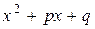 — неприводимый над полем
— неприводимый над полем 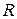 полином,
полином, 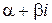 и
и 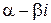 – его корни,
– его корни, 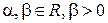 . Рассмотрим квадратную матрицу
. Рассмотрим квадратную матрицу
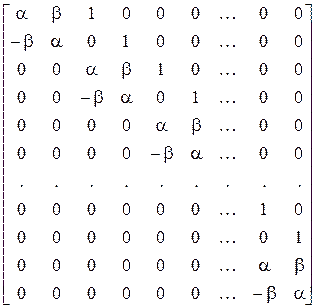
порядка 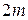 . Обозначим ее
. Обозначим ее 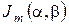 и назовем обобщенной клеткой Жордана. Эту матрицу можно записать в виде
и назовем обобщенной клеткой Жордана. Эту матрицу можно записать в виде
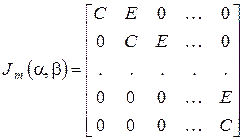 ,
,
где клетка
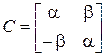
повторяется на “диагонали” 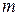 раз, а
раз, а 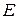 и
и 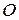 — единичная и нулевая матрицы второго порядка.
— единичная и нулевая матрицы второго порядка.
Например,
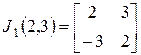 ,
, 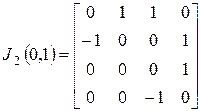 .
.
Квазидиагональную матрицу 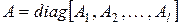 , каждая “диагональная” клетка
, каждая “диагональная” клетка 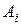 которой есть клетка Жордана или обобщенная клетка Жордана, назовем обобщенной жордановой матрицей. В частности, может быть
которой есть клетка Жордана или обобщенная клетка Жордана, назовем обобщенной жордановой матрицей. В частности, может быть 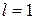 .
.
|
|
|
Пусть 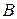 — квадратная матрица над полем
— квадратная матрица над полем 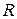 . Обобщенную жорданову матрицу, подобную матрице
. Обобщенную жорданову матрицу, подобную матрице 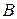 , назовем обобщенной жордановой нормальной формой матрицы
, назовем обобщенной жордановой нормальной формой матрицы 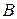 . Целью этого параграфа является доказательство существования обобщенной жордановой нормальной формы и получение алгоритма построения такой формы.
. Целью этого параграфа является доказательство существования обобщенной жордановой нормальной формы и получение алгоритма построения такой формы.
Теорема 9. Для всякой квадратной матрицы 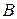 над полем действительных чисел существует обобщенная жорданова нормальная форма. Она определена однозначно с точностью до порядка следования “диагональных” клеток.
над полем действительных чисел существует обобщенная жорданова нормальная форма. Она определена однозначно с точностью до порядка следования “диагональных” клеток.
Если характеристический полином матрицы 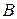 имеет лишь действительные корни, то существует над полем
имеет лишь действительные корни, то существует над полем 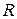 жорданова нормальная форма матрицы
жорданова нормальная форма матрицы 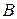 . Она будет искомой. Поэтому будем рассматривать случай, когда характеристический полином матрицы
. Она будет искомой. Поэтому будем рассматривать случай, когда характеристический полином матрицы 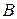 имеет недействительные корни. Доказательству нашей теоремы для этого случая предпошлем несколько лемм, заметив предварительно, что над полем
имеет недействительные корни. Доказательству нашей теоремы для этого случая предпошлем несколько лемм, заметив предварительно, что над полем 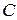 существует жорданова нормальная форма
существует жорданова нормальная форма 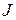 матрицы
матрицы 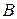 . Как и раньше, через
. Как и раньше, через 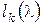 будем обозначать количество клеток Жордана
будем обозначать количество клеток Жордана 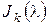 , стоящих на “диагонали” матрицы
, стоящих на “диагонали” матрицы 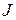 .
.
Лемма I. 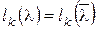 .
.
Доказательство. По формуле (*) § 4
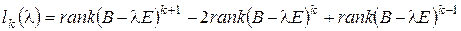 .
.
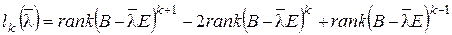 .
.
Следовательно, нам достаточно показать, что 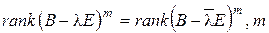 - натуральное. Нетрудно убедиться, что
- натуральное. Нетрудно убедиться, что 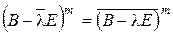 и, значит,
и, значит, 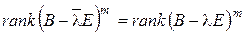 .
.
 2015-09-06
2015-09-06 23313
23313








