11. 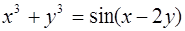
Ответ: 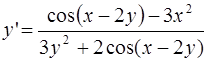
12. 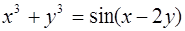
Ответ: 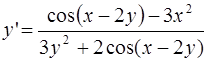
13. 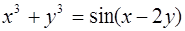
Ответ: 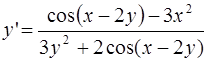
14. 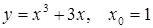 ; ;
| 15. 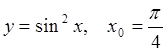 ; ;
|
16. 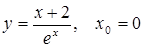 ; ;
| 17.  . .
|
Найти производные порядка 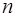
Если 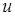 и
и 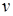 - функции, имеющие производные порядка
- функции, имеющие производные порядка 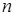 , то
, то
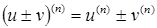 ;
;
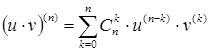 - формула Лейбница.
- формула Лейбница.
18. 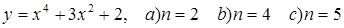 ;
;
19. 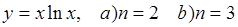 ;
;
20. 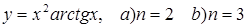 ;
;
21. 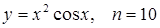 ;
;
22. 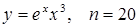 ;
;
23. 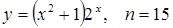 ;
;
24. 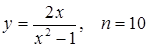 ;
;
25. 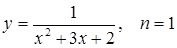 .
.
Составить уравнения касательных и нормалей к кривым
Уравнение касательной к кривой 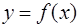 в точке
в точке 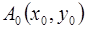 имеет вид
имеет вид
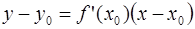 , а уравнение нормали –
, а уравнение нормали – 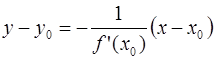
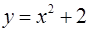 в точке
в точке 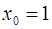
Касательная 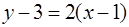
Нормаль 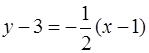
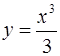 в точке
в точке 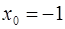
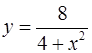 в точке
в точке 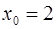
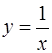 в точке
в точке 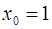
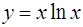 в точке
в точке 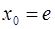
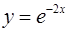 в точке
в точке 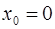
Найти дифференциалы функций
Если 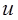 и
и 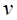 дифференцируемые функции от
дифференцируемые функции от 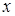
26. 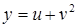 ; ;
| 27. 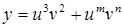 ; ;
|
28. 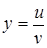 ; ;
| 29. 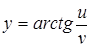 ; ;
|
30. 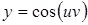 ; ;
| 31. 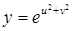 . .
|
Вычислить приближенно
32. 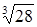 ; ;
| 33. 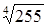 ; ;
|
34.  ; ;
| 35. 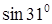 ; ;
|
36. 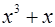 при при 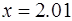
| 37. 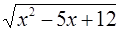 при при 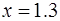
|
38. 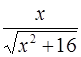 при при 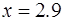
| 39. 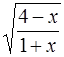 при при 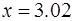
|
Вычислить пределы с использованием правила Лопиталя
40. 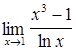 ; ;
| 41. 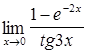 ; ;
|
42. 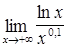 ; ;
| 43. 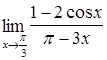 ; ;
|
44. 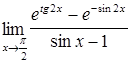 ; ;
| 45. 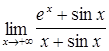 ; ;
|
46. 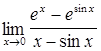 ; ;
| 47. 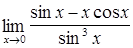 ; ;
|
48. 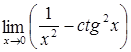 ; ;
| 49. 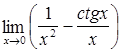 ; ;
|
50. 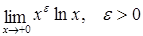 ; ;
| 51. 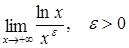 ; ;
|
52. 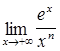 ; ;
| 53. 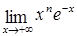 ; ;
|
54. 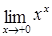 ; ;
| 55. 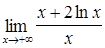 ; ;
|
56. 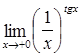 ; ;
| 57. 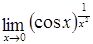 ; ;
|
58.  ; ;
| 59. 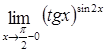 . .
|
Исследование функций одной переменной
Контрольные вопросы к теме
1. Критерии монотонности функции.
2. Необходимое и достаточное условия существования экстремума функции.
3. Понятие стационарных точек функции.
|
|
|
4. Области выпуклости графика функции и точки перегиба.
5. План исследования функции и построение ее графика.
6. Интерполяция и аппроксимация функций.
7. Интерполяционный полином Лагранжа.
8. Формула Тейлора и формула Маклорена.
9. Понятие эмпирических функций.
Найти асимптоты кривой
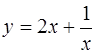
Решение:
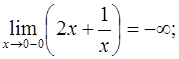
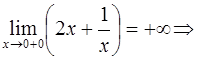
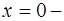 вертикальная асимптота
вертикальная асимптота
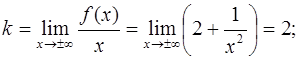
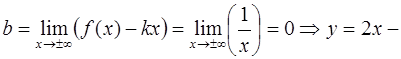 наклонная асимптота при
наклонная асимптота при 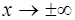
Исследовать функцию и построить график:
Пример. План исследования функции и построения ее графика рассмотрим на примере функции 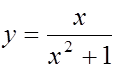 .
.
I. Область определения X = R.
Функция не является периодической.
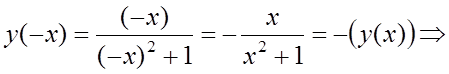 функция четная
функция четная
II. 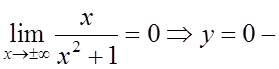 асимптота, причем,
асимптота, причем,
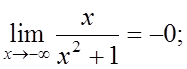
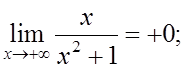
Так как y (x)® + ¥ при x ®+¥ и y ®-¥ при x ®-¥, то возможно существование наклонных асимптот (негоризонтальных).
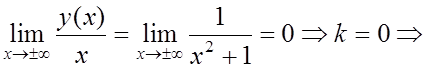 кроме горизонтальной асимптоты
кроме горизонтальной асимптоты  наклонных асимптот нет
наклонных асимптот нет
III. Найти локальные экстремумы функции
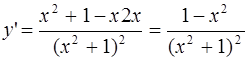 ;
;
Из уравнения 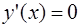 находим стационарные точки при x = 1 и x = –1
находим стационарные точки при x = 1 и x = –1
IV. Найти точки перегиба функции
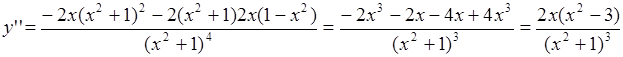
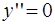 при
при 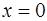 ,
,  и
и 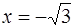 (точки перегиба)
(точки перегиба)
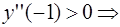 при
при 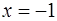 - максимум;
- максимум; 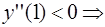 при
при 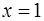 – минимум
– минимум
V. Строим таблицу, в которой выделены промежутки однообразного поведения функции и ее характерные точки.
| x | (-¥;- 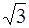 ) )
| – 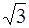
| (– 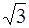 ;1) ;1)
| –1 | (–1;0) | |
| y'(x) | – | – | – | + | + | |
| y''(x) | – | + | + | + | ||
| min | ||||||
    
| точка пере-гиба | точка пере-гиба |
| x | (0;1) | (1; 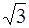 ) )
| 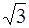
| (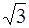 ;¥) ;¥)
| ||
| y'(x) | + | + | – | – | – | |
| y''(x) | – | – | – | + | ||
| max | ||||||
| точка пере-гиба | 
|  
| 
| точка пере-гиба | 
|
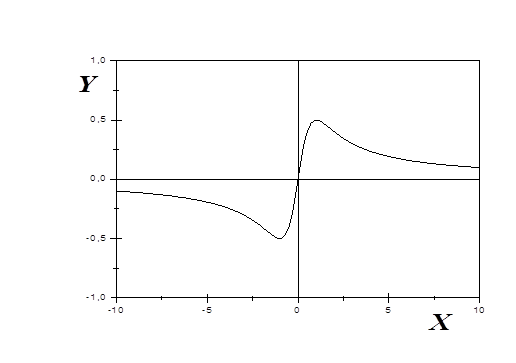
Построить графики функций:
1. 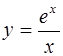
| 2. 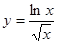
|
3. 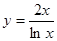
| 4. 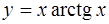
|
5. 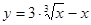
| 6. 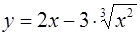
|
7. 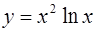
| 8. 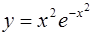
|
 2015-10-13
2015-10-13 670
670








