Пример:
Наглядный материал: Игрушки в коробке.
Вопрос ребенку: «Есть ли в коробке мячи?»
Математическое предложение: «Хотя бы один из предметов – мяч».
| Вариант ответа | Установление значение истинности |
| Да | Показ хотя бы одного мяча (конкретный пример). |
| нет | Просмотр каждой игрушки (доказательство). |
Операция получения высказываний из высказывательных форм (предикатов) с помощью кванторов называется операцией навешивания кванторов.
Итак, если задана одноместная высказывательная форма Р(х), заданная на множестве Х, то чтобы превратить ее в высказывание, нужно связать квантором общности или существования содержащуюся в ней переменную. Если высказывательная форма содержит несколько переменных, то перевести ее в высказывание можно, связав квантором каждую переменную.
Например, если дана высказывательная форма Р(х; у): «х + у =5», х, у ÎN, то для получения высказывания надо связать кванторами каждую переменную: 1)(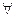 x ÎN) (
x ÎN) (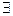 у ÎN) (x + у =5); 2) (
у ÎN) (x + у =5); 2) (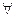 x, у ÎN) (x + у =5); 3) (
x, у ÎN) (x + у =5); 3) (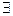 x, у ÎN)(x + у =5).
x, у ÎN)(x + у =5).
|
|
|
Из полученных высказываний первое и третье будут истинны, а второе – ложно.
Однако важно уметь не только переходить от высказывательных форм (предикатов) к высказываниям с кванторами, но и распознавать высказывания, содержащие кванторы, и выявить их логическую структуру. Дело в том, что в формулировках определений, теорем и других математических предложений кванторы только подразумеваются, а явно не используются.
Например, в формулировке теоремы «Диагонали ромба взаимно перпендикулярны» квантора в явном виде нет, но предполагается, что данное утверждение верно для всех ромбов.
Задача.
Выявить логическую структуру следующих высказываний:
1. Некоторые натуральные числа делятся на 3.
2. Произведение двух последовательных натуральных чисел кратно 2.
3. В прямоугольнике диагонали равны.
Решение:
1. В этом предложении имеется квантор существования, выраженный словом «некоторые» и высказывательная форма «числа делятся на 3», заданная на множестве N натуральных чисел. Обозначив эту форму символом А(х), получим логическую структуру данного предложения: (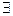 х ÎN) А(х). Если А(х) записать, используя символ: «х M3», то исходное высказывание можно представить в виде: (
х ÎN) А(х). Если А(х) записать, используя символ: «х M3», то исходное высказывание можно представить в виде: (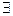 х ÎN)(х M3).
х ÎN)(х M3).
2. В данном высказывании подразумевается квантор общности и имеется высказывательная форма «произведение двух последовательных чисел кратно 2», заданная на множестве N натуральных чисел. Обозначим ее А(х), тогда логическая структура данного высказывания такова: (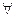 х ÎN) А(х). Если последовательные числа обозначить через х и х +1, то искомое высказывание можно представить в виде: (
х ÎN) А(х). Если последовательные числа обозначить через х и х +1, то искомое высказывание можно представить в виде: (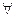 х ÎN) х (х +1) M2.
х ÎN) х (х +1) M2.
|
|
|
3. В данном высказывании квантора в явном виде нет, но он подразумевается, т.к. свойством «иметь равные диагонали» обладают любые прямоугольники, поэтому, этот квантор общности можно включить в высказывание, не изменив его сути: «В любом прямоугольнике диагонали равны». Тогда его структура такова: (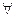 х ÎХ)А(х), где Х – множество прямоугольников, А(х) – высказывательная форма «в прямоугольнике х диагонали равны».
х ÎХ)А(х), где Х – множество прямоугольников, А(х) – высказывательная форма «в прямоугольнике х диагонали равны».
 2015-10-22
2015-10-22 1718
1718








