Элементы математической статистики

Основным содержанием математической статистики является систематизация, обработка и использование статистической информации для определения статистических закономерностей признака или признаков некоторой совокупности элементов.

Так как сплошная обработка всех элементов совокупности практически невозможна, то, как правило, используется выборочный метод. Отсюда, различают генеральную и выборочную совокупность.

Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.

Генеральной совокупностью называют совокупность объектов, из которых производится выборка.

Объемом совокупности (выборочной или генеральной) называют число объектов, из которых выполняется выборка.

Пусть для изучения количественного (дискретного или непрерывного) признака 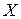из генеральной совокупности извлечена выборка , причем наблюдалось раз, раз, раз и , т.е. объем выборки равен . Наблюдаемые значения называют вариантами, а последовательность вариант, записанных в порядке возрастания – вариационным рядом.

Числа наблюдений называют частотами, а их отношения к объему выборки – относительными частотами.

Перчень вариант вариационного ряда и соответствующих им частот, или относительных частот, называют дискретным статистическим распределением выборки.

В табличной форме он имеет вид:

X = xi	x 1	x 2	x 3	…	xk
ni	n 1	n 2	n 3	…	nk
Wi	W 1	W 2	W 3	…	Wk

Полигоном частот называют ломанную, отрезки которой соединяют точки , , …, , где –варианты выборки и – соответствующие им частоты.

Полигоном относительных частот называют ломанную, отрезки которой соединяют точки , где –варианты выборки и – соответствующие им относительные частоты.

Эмпирической функцией распределения называют функцию , определяющую для каждого значения 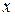относительную частоту события :

,

где – число вариант, меньших .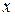

Эмпирическая функция обладает следующими свойствами:

Свойство 1. Значения эмпирической функции принадлежат отрезку .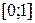

Свойство 2. – неубывающая функция.

Свойство 3. Если – наименьшая варианта, а – наибольшая, то при и при .

Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, которыми определяется это распределение.

Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.

Точечной называют статистическую оценку, которая определяется одним числом.

Наилучшей называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.

Наилучшей оценкой генеральной средней служит выборочная средняя

,

где – варианта выборки, – частота варианты , – объем выборки.

Наилучшей оценкой генеральной дисперсии служит исправленная выборочная дисперсия

.

Модой называют варианту, которая имеет наибольшую частоту.

Например для ряда

мода равна 5.

Медианой 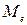называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно, то центр вариационного ряда и есть медиана; если число вариант четно, то медиана равна полусумме двух центральных вариант.

Например, для ряда медиана равна 5; для ряда медиана равна .

Размахом варьирования 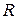называют разность между наибольшей и наименьшей вариан-тами:

.

Например, для ряда размах равен .

Задачи типа 431-440.

Õ Пример. При изучении случайной величины Х в результате 40 независимых наблюдений получили выборку

10, 13, 10, 9, 9, 12, 12, 6, 7, 9, 8, 9, 11, 9, 14, 13, 9, 8, 8, 7, 10, 10, 11, 11, 11, 12, 8, 7, 9, 10, 14, 13, 8, 8, 9, 10, 11, 11, 12, 12.

Необходимо:

1. Построить дискретное статистическое распределение для этой выборки, а также полигон относительных частот.

2. Найти: 1) выборочную среднюю 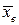и среднее квадратическое отклонение ;

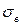2) моду 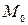, медиану 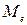и размах варьирования ;

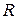Решение. 1.

Построим дискретное статистическое распределение

Найдем относительные частоты, для чего разделим частоты на объем выборки:

.

Запишем распределение относительных частот:

	1/40	3/40	6/40	8/40	6/40	6/40	5/40	3/40	2/40

Контроль: .

Отложим на оси абсцисс варианты , а на оси ординат – соответствующие им относительные частоты . Соединив точки отрезками прямых, получим искомый полигон относительных частот рис.1.

Рис. 1.

2.1. Так как , то в соответствии с вышеприведенными формулами получим выборочную среднюю

.

Для вычисления определим

Тогда

.

.

Среднеквадратическое отклонение

2.2. В данном статистическом распределении мода равна , так как эта варианта имеет наибольшую частоту появления

Медиана в приведенном примере равна , так как варианта делит вариационный ряд на две части, которые имеют одинаковое количество вариант

и .

Размах варьирования будет n