Содержание отчета по результатам

Таблица 4

В отчете по результатам содержатся оптимальные значения переменных Х₁, Х₂, Х₃, Х₄, которые соответственно равны 0; 10; 30; 0; значение целевой функции - 150, а также левые части ог­раничений.

Содержание остальных отчетов будет рассмотрено ниже.

3. Сформулируем экономико-математическую модель двойственной задачи к задаче о коврах.

Неизвестные. Число неизвестных в двойственной задаче равно числу функциональных ограничений в исходной задаче. Исход­ная задача содержит 3 ограничения: по труду, сырью и оборудо­ванию. Следовательно, в двойственной задаче 3 неизвестных:

Y₁ - двойственная оценка ресурса «труд», или «цена» труда; Y₂ - двойственная оценка ресурса «сырье», или «цена» сырья; Y₃ - двойственная оценка ресурса «оборудование», или «цена» оборудования.

Целевая функция двойственной задачи формулируется на ми­нимум. Коэффициентами при неизвестных в целевой функции двой­ственной задачи являются свободные члены в системе ограничений исходной задачи: g(Y) = 80Y₁ + 480Y₂ + 130Y₃ → min.

Необходимо найти такие «цены» на ресурсы (Y_i), чтобы общая стоимость используемых ресурсов была минимальной.

Ограничения. Число ограничений в системе двойственной за­дачи равно числу переменных в исходной задаче. В исходной задаче 4 переменных, следовательно, в двойственной задаче 4 огра­ничения. В правых частях ограничений двойственной задачи стоят коэффициенты при неизвестных в целевой функции исходной задачи. Левая часть ограничений определяет стоимость ресурсов, затрачен­ных на производство единицы продукции. Каждое ограничение соответствует определенному виду продукции:

7Y₁ + 5Y₂ + 2Y₃ ≥ 3,

2Y₁ + 8Y₂ + 4Y₃ ≥ 4,

2Y₁ + 4Y₂ + Y₃ ≥ 3,

6Y₁ + 3Y₂ + 8Y₃ ≥ 1,

Y₁, Y₂, Y₃ ≥ 0.

4. Найдем оптимальный план двойственной задачи, используя теоремы двойственности.

Воспользуемся первым соотношением второй теоремы двой­ственности

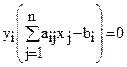, тогда

Y₁∙(7Х₁ + 2Х₂ + 2Х₃ + 6Х₄ - 80) = 0,

Y₂∙(5Х₁ + 8Х₂ + 4Х₃ + 3Х₄ - 480) = 0,

Y₃∙(2Х₁ + 4Х₂ + Х₃ + 8Х₄ - 130) = 0.

Подставим оптимальные значения вектора Х в полученные вы­ражения

Y₁∙(7∙0 + 2∙30 + 2∙10 + 6∙0 - 80) = 0,

Y₂∙(5∙0 + 8∙30 + 4∙10 + 3∙0 - 480) = 0,

Y₃∙(2∙0 + 4∙30 + 1∙10 + 8∙0 - 130) = 0

и получим

Y₁∙(80 - 80) = 0,

Y₂∙(280 - 480) = 0, так как 280 < 480, то Y2 = 0,

Y₃∙(130 - 130) = 0.

Воспользуемся вторым соотношением второй теоремы двой­ственности

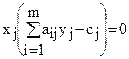; если x_j > 0, то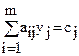

В нашей задаче Х₂ = 30 > 0 и Х₃ = 10 > 0, поэтому второе и третье ограничения двойственной задачи обращаются в равенства

2∙Y₁ + 8∙Y₂ + 4∙Y₃ = 4,

2∙Y₁ + 4∙Y₂ + 1∙Y₃ = 3,

Y₂ = 0.

Решая полученную систему уравнений, находим Y₁ и Y₃. Теневые цены ресурсов «труд», «сырье» и «оборудование» со­ответственно равны Y₁ = 4/3, Y₂ = 0, Y₃ = 1/3, или в десятичных дробях 1.3333; 0; 0.3333.

Проверим выполнение первой теоремы двойственности

g(Y) = 80∙Y₁ +480∙Y₂ + 130∙Y₃ = 80∙4/3 + 480∙0 + 130∙1/3 = 150,

f (Х) = 3∙Х₁ +4∙Х₂ +3∙Х₃ + Х₄ = 3∙0 + 4∙30 + 3∙10 + 0 = 150.

Это означает, что оптимальный план двойственной задачи определен верно.

Ответ на вопрос о равенстве нулю Х₁ и Х₄ будет дан позже.

Решение двойственной задачи можно найти, выбрав команду Поиск решений => Отчет по устойчивости.

Отчет по устойчивости. Отчет по устойчивости приводится в табл. 1.5. Первая часть таблицы содержит информацию, относя­щуюся к переменным:

§ Результат решения задачи.

§ Нормированная стоимость, которая показывает, на сколько изменится значение ЦФ в случае принудительного включения единицы этой продукции в оптимальное решение. Например, в отчете по устойчивости для рассматриваемой задачи (см. табл. 5) нормированная стоимость для ковров первого вида равна -7 тыс. руб./шт. (строка 1). Это означает, что если мы, несмотря на оптимальное решение (0; 30; 10; 0), попробуем включить в план выпуска один ковер первого вида, то новый план выпуска принесет нам доход 143 тыс. руб., что на 7 тыс. руб. меньше, чем прежнее оптимальное решение.

§ Коэффициенты целевой функции.

§ Предельные значения приращения целевых коэффициентов Δc_j, при которых сохраняется первоначальное оптимальное реше­ние. Например, допустимое увеличение цены на ковер первого вида равно 7 тыс. руб./шт., а допустимое уменьшение – практически не ограничено (строка 1 из табл. 5). Это означает, что если цена ковра первого вида возрастет более чем на 7 тыс. руб./шт., то оптимальное решение изменится: станет целесообразным вы­пускать X₁. А если их цена будет снижаться вплоть до нуля, то оптимальное решение (0; 30; 10; 0) останется прежним.

Во второй части табл. 5 содержится информация, относя­щаяся к ограничениям:

§ Величина использованных ресурсов в колонке Результ. значение.

§ Предельные значения приращения ресурсов Δb_i. В графе Допустимое уменьшение показано, на сколько можно уменьшить (устранить излишек) или увеличить (повысить минимально необходимое требование) ресурс, сохранив при этом оптималь­ное решение. Рассмотрим анализ дефицитных ресурсов. Ана­лизируя отчет по результатам, мы установили, что существуют причины (ограничения), не позволяющие фабрике выпускать больше ковров, чем в оптимальном решении, и получать более высокий доход. В рассматриваемой задаче такими ограниче­ниями являются дефицитные ресурсы «труд» и «оборудование». Поскольку знак ограничений этих запасов имеет вид ≤, то возникает вопрос, на сколько максимально должен возрасти запас этих ресурсов, чтобы обеспечить увеличение выпуска продукции. Ответ на этот вопрос показан в графе Допустимое увеличение. Ресурс «труд» имеет смысл увеличить самое большее на 150 чел./дней, а ресурс «оборудование» - на 30 станко/час.

§ Ценность дополнительной единицы ресурса i («теневая цена») рассчитывается только для дефицитных ресурсов.

Таблица 5