Оценка результата и погрешностей косвенных измерений

Любой из аргументов функции можно представить в ви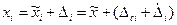де: , где 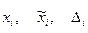- соответственно истинное значение, оценка и абсолютная погрешность результата измерения 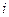-го аргумента, а параметры 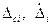- систематическая и случайная составляющие абсолютной погрешности.

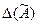Задача состоит в том, чтобы с помощью функции и ее аргументов найти оценки результата косвенного измерения и его погрешности в виде:

,

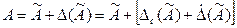где 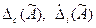- систематическая и случайная составляющие погрешности косвенного измерения. Для решения задачи подставим в выражение функции значения аргументов, и получим выражение:

Положим, что в последней формуле погрешности 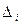аргументов малы по сравнению с оценкой 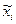аргументов и что в пределах изменения 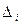допустима линеаризация функции. Учитывая это, разложим данную функцию в ряд Тейлора и оставим в нем только члены первого порядка:

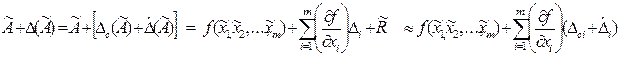
где 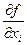- частные производные, вычисляемые при оценках 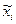; 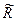- остаточный член ряда Тейлора .

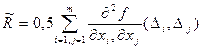Из функции, разложенной в ряд Тейлора, получим формулу для оценки результата косвенного измерения 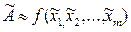, а также выражение для оценки его абсолютной систематической погрешности 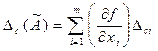, в котором частные производные 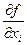называют коэффициентами влияния 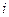-го аргумента, а слагаемые 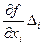- частными погрешностями.

На практике систематические погрешности 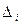аргументов стремятся устранить. А их неисключенные остатки рассматриваются как случайные, подчиняющиеся равномерному закону распределения. Поэтому выражение для оценки систематической погрешности косвенного измерения, отличается от вышеприведенного.

Для оценки случайной составляющей берем выражение 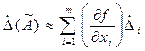и усредняем квадраты левой и правой частей, что позволяет в итоге найти оценку СКО 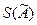случайной погрешности результата косвенного измерения в зависимости от оценок СКО 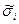случайных погрешностей аргументов:

,

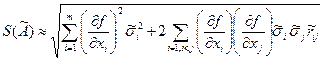где 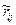- оценка коэффициента корреляции, определяющего меру статистической связи случайных величин 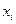и 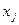. Все возможные значения оценки коэффициента корреляции 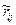лежат в интервале от -1 до +1. Установление значения 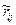обычно затруднительно. Поэтому рассматриваются два случая: 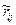=1 (полная статистическая связь между аргументами) и 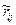=0 (отсутствие связи).

При 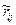=0 оценку СКО 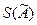вычисляют по формуле .

Для использования выражений, применяющихся для вычисления СКО 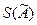, требуются вычисления оценок СКО 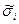аргументов функции на основе обработки результатов их многократных наблюдений.

Рассмотрим частные случаи вычисления СКО косвенного измерения при отсутствии корреляции между погрешностями измерения аргументов.

1. Пусть функция имеет вид суммы . Найдя ее частные производные 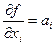и подставив их в выражение 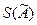, получим: .

2. Пусть функция имеет вид произведения 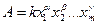, где - константы.

Определим ее частные производные по аргументам 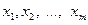и подставим их в выражение 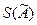. После преобразований получим удобное для расчетов выражение:

,

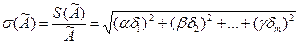где 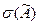и 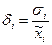- соответственно относительные СКО случайных погрешностей результата измерения и 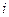-го аргумента.