Этот метод предусматривает для решения метрических задач последовательное изменение положения плоскости проекций V на 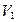 и плоскости проекции Н на
и плоскости проекции Н на 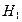 , причем при каждом изменении одной из этих плоскостей рассматриваемые геометрические объекты проектируются на две взаимно-перпендикулярные плоскости.
, причем при каждом изменении одной из этих плоскостей рассматриваемые геометрические объекты проектируются на две взаимно-перпендикулярные плоскости.
При решении задач, когда необходимо использовать метод перемены двух плоскостей проекций, условие задания обычно даётся на ортогональном чертеже в системе плоскостей проекций 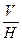 представленной осью
представленной осью 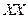 .
.
Основываясь на необходимости выполнения задания, мы связываем на ортогональном чертеже заданную систему 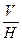 с новой ––
с новой –– 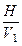 , которая представлена осью
, которая представлена осью 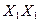 , где плоскость проекций Н остаётся в прежнем состоянии, а плоскость V занимает новое положение
, где плоскость проекций Н остаётся в прежнем состоянии, а плоскость V занимает новое положение 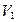 , оставаясь при этом перпендикулярной плоскости Н.
, оставаясь при этом перпендикулярной плоскости Н.
И, наконец, сообразуясь с требованиями задачи, обе эти системы связываем с системой плоскостей 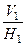 , представленной на нашем ортогональном чертеже осью
, представленной на нашем ортогональном чертеже осью 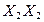 , где плоскость проекций
, где плоскость проекций 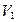 остается неизменной, а плоскость Н, занимая новое положение
остается неизменной, а плоскость Н, занимая новое положение 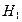 , остаётся перпендикулярной плоскости
, остаётся перпендикулярной плоскости 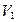 .
.
|
|
|
На ортогональном чертеже рисунка 84 показана точка А в системе 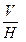 :
: 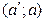 . При
. При
переходе к системе 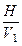 , обозначенной осью
, обозначенной осью 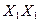 , положение проекции
, положение проекции  в плоскости Н остается неизменной, а проекция на новую плоскость
в плоскости Н остается неизменной, а проекция на новую плоскость 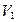 переносится известным образом в точку
переносится известным образом в точку 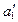 . Проекции точки А в системе
. Проекции точки А в системе 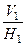 , обозначенной осью
, обозначенной осью 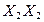 :
: 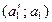 ; здесь
; здесь
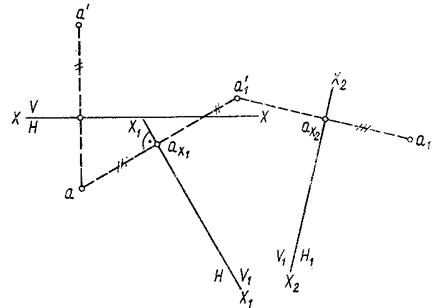
Рис. 84.
позиция проекции 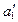 неизменна, а проекция на новую плоскость
неизменна, а проекция на новую плоскость 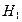 известным методом переносится в точку
известным методом переносится в точку 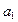 (см. рис. 84). Рассмотрим на конкретном примере решение задачи, пользуясь переменой двух плоскостей проекций.
(см. рис. 84). Рассмотрим на конкретном примере решение задачи, пользуясь переменой двух плоскостей проекций.
Задача 1. Определить расстояние от точки 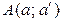 до прямой
до прямой 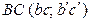 (рис. 85).
(рис. 85).
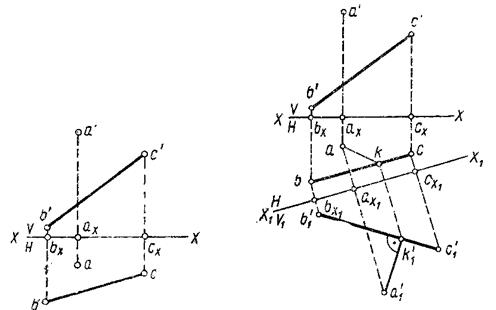
Рис. 85 Рис. 86
Ре ш е н и е. Расстояние от точки до прямой выражается отрезком перпендикуляра, опущенного из данной точки на данную прямую и ограниченного данной точкой и точкой его пересечения с прямой, т.е. необходимо прежде всего опустить из точка 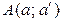 на прямую
на прямую 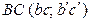 перпендикуляр и найти его основание.
перпендикуляр и найти его основание.
Прямой угол между данной прямой ВС и прямой к ней перпендикулярной, будет проектироваться без искажения на плоскость, параллельную данной прямой. Следовательно, прежде всего необходимо выбрать новую плоскость проекций, параллельную прямой 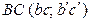 : выбираем новую плоскость
: выбираем новую плоскость 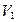 , параллельную прямой ВС, такому выбору плоскости на ортогональном чертеже (рис. 86) соответствует выбор новой оси
, параллельную прямой ВС, такому выбору плоскости на ортогональном чертеже (рис. 86) соответствует выбор новой оси 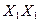 параллельно проекции
параллельно проекции 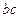 .
.
Строим уже известным образом на новой плоскости проекций 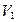 проекции точки
проекции точки 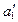 и проекцию прямой
и проекцию прямой 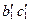 . Затем из точки
. Затем из точки 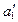 на проекцию прямой
на проекцию прямой 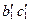 опускаем перпендикуляр и находим его основание
опускаем перпендикуляр и находим его основание 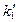 –– точка
–– точка 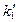 является проекцией на плоскость
является проекцией на плоскость 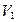 основания перпендикуляра
основания перпендикуляра 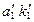 , опущенного из данной точки на данную прямую.
, опущенного из данной точки на данную прямую.
|
|
|
Для построения проекции на плоскость Н этого перпендикуляра 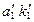 , через точку
, через точку 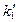 проводим прямую, перпендикулярную к оси
проводим прямую, перпендикулярную к оси 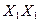 (линию проекционной связи) до пересечения в точке
(линию проекционной связи) до пересечения в точке 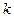 с проекцией bc, и точку а соединяем с точкой
с проекцией bc, и точку а соединяем с точкой 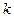 (рис. 86).
(рис. 86).
Отрезки 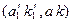 являются проекциями расстояний от данной точки А до заданной прямой ВС соответственно в плоскостях проекций
являются проекциями расстояний от данной точки А до заданной прямой ВС соответственно в плоскостях проекций 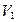 и Н, но это ещё не истинное расстояния от точки А до прямой ВС, а только её проекции.
и Н, но это ещё не истинное расстояния от точки А до прямой ВС, а только её проекции.
Последним этапом решения задачи является определение истинной длины отрезка 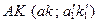 , который является искомым расстоянием. Указанный отрезок будет проектироваться без искажения на плоскость ему параллельную. Следовательно, для окончательного решения задачи необходимо выбрать новую плоскость проекций
, который является искомым расстоянием. Указанный отрезок будет проектироваться без искажения на плоскость ему параллельную. Следовательно, для окончательного решения задачи необходимо выбрать новую плоскость проекций 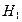 , параллельную отрезку
, параллельную отрезку 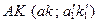 (рис. 87).
(рис. 87).
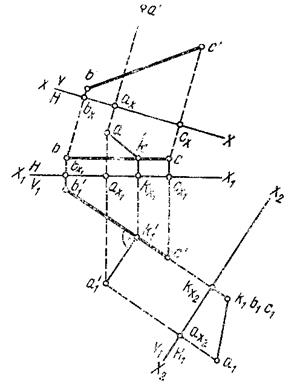
Рис. 87
В качестве новой плоскости проекций выбираем плоскость 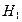 На ортогональном чертеже выбору этой плоскости соответствует выбор новой оси
На ортогональном чертеже выбору этой плоскости соответствует выбор новой оси 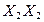 параллельно проекции
параллельно проекции 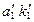 [13]. Построенную новую систему плоскостей проекций
[13]. Построенную новую систему плоскостей проекций 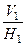 с осью
с осью 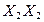 свяжем на ортогональном чертеже рисунка 85 с системами
свяжем на ортогональном чертеже рисунка 85 с системами 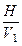 и
и 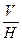 .
.
Строим в плоскости 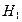 системы
системы 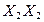 проекцию отрезка
проекцию отрезка 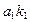 , откладывая для получения проекции каждой точки этого отрезка соответственно расстояния от оси
, откладывая для получения проекции каждой точки этого отрезка соответственно расстояния от оси 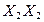 : для получения точки
: для получения точки 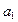 –
– 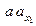 , а для точки
, а для точки 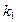 –
– 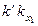 . Нужно отметить, что проекция прямой ВС на плоскости проекций
. Нужно отметить, что проекция прямой ВС на плоскости проекций 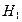
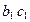 проектируется в точку, совпадая с проекцией
проектируется в точку, совпадая с проекцией 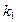 , т.к. в пространстве плоскость
, т.к. в пространстве плоскость 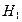 перпендикулярна к прямой ВС (см. рис. 87).
перпендикулярна к прямой ВС (см. рис. 87).
Длина проекции 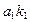 является истинной длиной расстояния от точки А до прямой ВС –– задача решена.
является истинной длиной расстояния от точки А до прямой ВС –– задача решена.
Задача 2. Найти расстояние между двумя параллельными прямыми 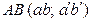 и
и 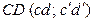 (рис. 88).
(рис. 88).
Р е ш е н и е. Искомое расстояние выражается отрезком перпендикуляра, проведённого к обеим данным параллельным прямым и ограниченного точками пересечения с этими прямыми при параллельности плоскости, образованной этими параллельными прямыми, какой-то плоскости проекций.
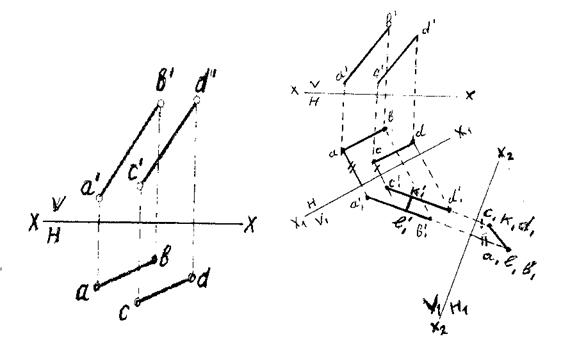
Рис. 88 Рис. 89
Для осуществления первого этапа решения задачи выбираем новую плоскость проекций 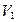 , параллельную плоскости, образованных этими прямыми. Такому выбору плоскости на ортогональном чертеже рисунка 89 соответствует выбор новой оси
, параллельную плоскости, образованных этими прямыми. Такому выбору плоскости на ортогональном чертеже рисунка 89 соответствует выбор новой оси 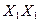 параллельной данным параллельным прямым
параллельной данным параллельным прямым 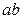 и
и 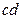 .
.
Известным методом в новой плоскости проекций 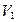 строим проекции прямых
строим проекции прямых 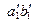 и
и 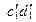 .
.
Вторым этапом решения задачи является определение истинного расстояния между параллельными прямыми 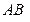 и
и 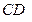 .
.
Для окончания решения задачи необходимо выбрать новую плоскость проекций 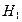 ,
,
перпендикулярную к данным прямым 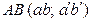 и
и 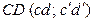 . На ортогональном чертеже выбору этой плоскости соответствует выбор новой оси
. На ортогональном чертеже выбору этой плоскости соответствует выбор новой оси 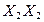 системы
системы 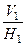 (рис. 89). Находим проекцию отрезка
(рис. 89). Находим проекцию отрезка 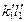 , который является взаимным перпендикуляром к заданным параллельным прямым.
, который является взаимным перпендикуляром к заданным параллельным прямым.
В плоскости 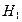 строим прямую
строим прямую 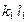 , которая является истинным расстоянием между заданными прямыми
, которая является истинным расстоянием между заданными прямыми 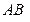 и
и 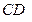 .
.
Следует обратить внимание, что проекции на плоскости 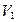 точек прямой
точек прямой 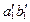 проектируются в одну точку вместе с проекцией
проектируются в одну точку вместе с проекцией 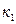 , а точек прямой
, а точек прямой 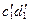 –– вместе с
–– вместе с 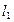 (рис. 89).
(рис. 89).
ПРОЕКТИРОВАНИЕ ГЕОМЕТРИЧЕСКИХ ПОВЕРХНОСТЕЙ
И ГЕОМЕТРИЧЕСКИХ ТЕЛ
Геометрические тела, с которыми приходится встречаться в инженерной практике, могут быть разделены на два класса:
1. Геометрические тела с кривыми поверхностями. Это поверхности вращения: конус, цилиндр, сфера-шар.
2. Геометрические тела с многогранными поверхностями или многогранники: призма, пирамида.
ПОВЕРХНОСТИ ВРАЩЕНИЯ
Поверхности вращения образуются вращением линии 1 вокруг прямой i – оси вращения. Определитель поверхности вращения включает образующую 1 и ось i. Каждая точка образующей описывает при вращении окружность, плоскость которой перпендикулярна оси вращения. Эти окружности называются параллелями (h). Наибольшую и наименьшую параллели конуса называют соответственно экватором и горлом. Кривые, образующиеся на поверхности вращения в результате пересечения поверхности плоскостями, проходящими через ось вращения, называют меридианами. Точки на поверхности вращения обычно строят с помощью параллелей h и образующих 1.
|
|
|
Цилиндр образуется вращением прямой 1 вокруг параллельной ей оси i (рис. 1).
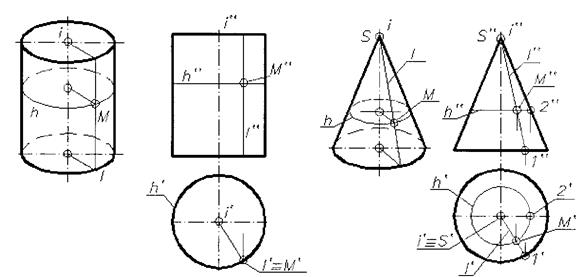
Рис. 1 Рис. 2
Конус образуется вращением прямой 1 вокруг пересекающейся с ней оси i (рис. 2).
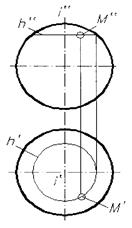 На этих же рисунках показано определение точки М, принадлежащей поверхностям цилиндра и конуса.
На этих же рисунках показано определение точки М, принадлежащей поверхностям цилиндра и конуса.
Сфера (шар) образуется вращением окружности вокруг её диаметра (рис. 3). Построение точек на сфере выполняют с помощью параллелей h. Наибольшая параллель сферы (круга) проходит через центр сферы и называется экватором. Если нужно найти точку М, принадлежащую поверхности сферы, то через заданную проекцию этой точки проводится проекция параллели h, затем находится вторая проекция этой параллели, после чего на ней с помощью линии связи строится недостающая проекция точки М.
МНОГОГРАННИКИ
Призма – многогранник, у которого две грани основания одинаковые и взаимно параллельные многоугольники, а остальные грани (боковые) – параллелограммы (рис. 3а). Рис. 3
Пирамида – многогранник, у которого одна грань, которая
принимается за основание, является произвольным многоугольником,
а остальные грани (боковые) – треугольники с общей точкой, которая
называется вершиной S (рис. 3б).
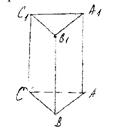
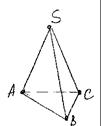
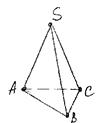
Рис. 3 а Рис. 3 б
Призма. Пирамида.
АВС – нижнее основание. S – вершина.
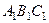 – верхнее основание. АВС – основание.
– верхнее основание. АВС – основание.
АВ 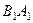 – грань. ABS – грань.
– грань. ABS – грань.
В 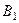 – ребро. SB – ребро.
– ребро. SB – ребро.
 2017-10-25
2017-10-25 402
402








