Тема 1.4. Непрерывность функции

 

Понятие непрерывности функции, так же как и понятие предела, является одним из основных понятий математическогоанализа.

Определение. Функцияf(х) называется непрерывной в точкеx₀, если она удовлетворяет следующим трем условиям:

1) определена в точкеx₀(т.е. существуетf(х ₀));

2) имеет конечный предел функции при х → х ₀;

3) этот предел равен значению функции в точке х ₀, т.е.

 

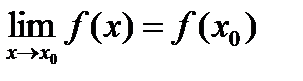
Пример 7. Исследовать непрерывность в точке х = 0 заданной функции: .

Решение:

а) В точке x =0 y = f (x) не является непрерывной, так как нарушено первое условие непрерывности – существование f (0).

Рисунок 3 – График функции

 

Функция f (x) непрерывна на отрезке, если она непрерывна в каждой точке этого отрезка.

Точка х ₀ называется точкой разрыва функции f (х), если эта функция в данной точке не является непрерывной. Различают точки разрыва:

первого рода (когда существуют конечные односторонние пределы функции слева и справа при х → х ₀, не равные друг другу);

Если , то х ₀ – точка разрыва I рода.

второго рода (когда хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует).

Если то точка х ₀– точка разрыва II рода.

устранимого разрыва, когда предел функции при х → х ₀ существует, но неравен значению функции в этой точке.

Если то в точке х ₀ – устранимый разрыв.

 

Нахождение асимптот

 

Асимптотой графика функции у = f(x) – называется прямая, обладающая тем свойством, что расстояние от точки до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. Асимптоты бывают: наклонные, горизонтальные, вертикальные.

 

Уравнение наклонной асимптоты находим в виде у = kх + b, где , .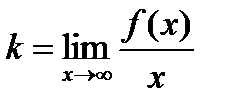

 

Пример 8. Исследовать график функции в точках х =1, х =2 и выполнить построение.

 

1) х =1 вертикальная асимптота, т.к. х =1 – точка разрыва (на нуль делить нельзя).

2) Определим вид разрыва в точке х =1

и 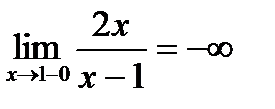следовательно х =1 точка разрыва II рода.

3) Находим наклонные асимптоты из уравнения у = kх + b

и 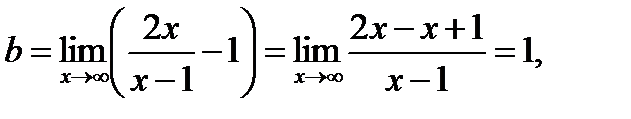итак у =1 – горизонтальная асимптота.

4) Исследуем поведение функции в точке х =2

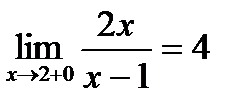и , и f (2)=4т.к. выполнены условия непрерывности функции в точке, функция в т. х =2 является непрерывной.

Построение:

1. На координатной прямой изобразили найденные асимптоты.

2. Обратили внимание на поведение функции справа и слева от точки разрыва.

3. При х=0 у=0 использовали уточняющее условие, для построения графика.

 

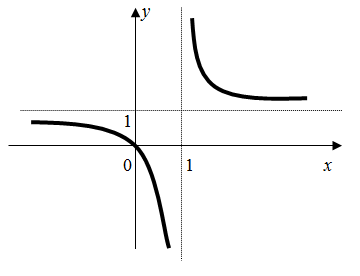
Рисунок 4 – График функции

 

Задания для самоконтроля

 

1. Вычислить пределы

а) 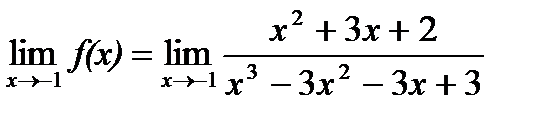.	и)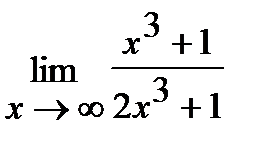
б) .	з)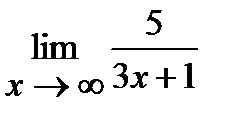
в) .	ж)
г) 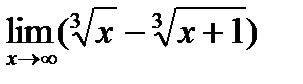.	м)
д)	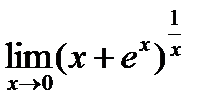н)
е) .	о)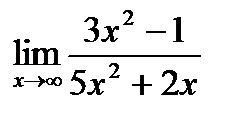
л)	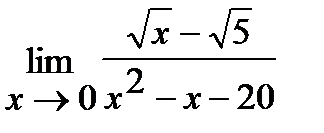п)
к)	р)

 

 

2. Исследовать непрерывность в точке х = 0 заданной функции: .

3. Исследовать функцию 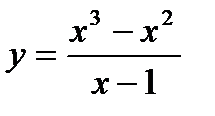на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.