Геометрический метод решения ЗЛП

При 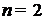ЗЛП принимает вид

(3.1)

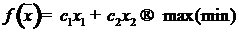. (3.2)

Рассмотрим 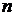-мерное координатное пространство с упорядоченными совокупностями (точками).

Определение 3.1. Множество точек пространства 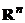, координаты которых удовлетворяют уравнению , где хотя бы одно из чисел (), отлично от нуля, называют гиперплоскостью пространства .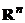

Определение 3.2. Множество точек пространства 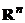, координаты которых удовлетворяют неравенству , называют полупространством пространства 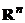, расположенным по одну сторону от

гиперплоскости .

В пространстве уравнение 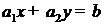определяет прямую, неравенство 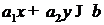определяет полуплоскость.

Определение 3.3. Множество точек пространства 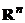, координаты которых одновременно удовлетворяют системе гиперплоскостей (), называют пересечением гиперплоскостей.

Определение 3.4. Выпуклой линейной комбинацией точек , , 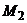…, пространства 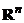называют точку (, ).

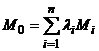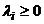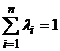Выпуклая линейная комбинация двух точек пространства 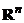является отрезком, соединяющим эти точки.

Определение 3.5. Множество точек пространства 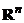называется выпуклым, если оно вместе с любыми двумя своими точками содержит и их произвольную линейную комбинацию (то есть содержит вместе с любыми двумя точками и 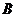все точки отрезка ).

Определение 3.6. Точку называют граничной точкой множества, если в любой сколь угодно малой окрестности точки содержатся как точки этого множества, так и точки, не принадлежащие ему.

Определение 3.7. Множество называют замкнутым, если оно содержит все свои граничные точки, в противном случае – открытым.

Определение 3.8. Точка называется угловой точкой выпуклого замкнутого множества, если она не может быть представлена в виде линейной комбинации каких-нибудь двух других различных точек этого множества.

Определение 3.9. Множество называют ограниченным, если существует шар радиусом конечной длины с центром в любой точке множества, который полностью содержит в себе данное множество. В противном случае множество называют неограниченным.

Определение 3.10. Множество называют св я зным, если любые две его точки можно соединить ломаной (или непрерывной кривой), целиком лежащей в этом множестве.

Определение 3.11. Открытое связное множество называют областью.

Определение 3.12. Если область содержит все свои граничные точки, то ее называют замкнутой областью.

Определение 3.13. Выпуклую замкнутую область, имеющую конечное число угловых точек, называют выпуклым 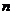-мерным многогранником.

Определение 3.14. Выпуклое замкнутое множество, имеющее конечное число угловых точек, называют выпуклой 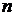-мерной многогранной

замкнутой областью.

Определение 3.15. Пересечением множеств называют множество точек, являющееся общей частью этих множеств.

Определение 3.16. Непустое множество допустимых решений ЗЛП называют многогранником планов (решений).

Определение 3.17. Угловую точку многогранника решений называют вершиной.

Определение 3.18. Вершину многогранника планов с неотрицательными координатами называют опорной. Соответствующий ей план называют опорным планом.

Из определений следует, что каждой вершине многогранника решений соответствует опорный план ЗЛП.

Определение 3.19. Опорный план называют невырожденным, если он содержит ровно 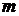положительных компонентов, и вырожденным, если положительных компонентов меньше .

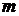Теорема 3.1 (основная теорема линейного программирования). Если ЗЛП имеет оптимальное решение, то целевая функция принимает экстремальное значение в одной из вершин многогранника планов. Если целевая функция принимает экстремальное значение более чем в одной вершине, то она принимает его в любой точке, являющейся их выпуклой линейной комбинацией.

Определение 3.20. Если целевая функция принимает экстремальное значение более чем в одной вершине многогранника планов, то говорят, что ЗЛП имеет альтернативный оптимум.

Определение 3.21. Совокупность точек, составляющих область допустимых решений, в случае двух управляющих переменных, называют многоугольником решений (планов).

Многоугольник решений может быть плоским многоугольником, неограниченным многоугольным множеством, отрезком. Геометрически ЗЛП представляет собой поиск такой точки многоугольника решений, координаты которой доставляют линейной целевой функции наибольшее или наименьшее значение, причем допустимыми решениями являются все точки многоугольника решений.