Смешанные задачи на комбинаторный подсчет вероятностей в классической схеме

2.63. В ящике находятся однотипные изделия, изготовленные раз­ными заводами; из них а изделий изготовлены заводом I, b изделий —
заводом II, с изделий — заводом III. Из ящика вынимают одно за
другим все находящиеся в нем изделия и отмечают места их изготов­ления. Найти вероятность того, что при этом изделие завода I появится раньше, чем изделие завода II.

2.64. Имеются два ящика, содержащих типовые элементы замены
(ТЭЗ). В первом ящике а исправных ТЭЗ и b неисправных; во втором —
с исправных и d неисправных. Из каждого ящика наугад вынимается
по одному ТЭЗ. Найти вероятность того, что оба ТЭЗ будут исправны­
ми.

2.65. В условиях задачи 2.64. найти вероятность того, что вынутые
ТЭЗ будут различными по качеству.

2.66. В тех же условиях найти вероятность того, что оба вынутых
ТЭЗ будут неисправны.

2.67. В ящике имеется k перенумерованных однотипных изделий
с номерами 1, 2,..., k. Из ящика l раз вынимается наугад по одному
изделию, его номер записывается и изделие кладется обратно в ящик.
Найти вероятность р того, что все записанные номера будут различны.

2.68. Из пяти букв разрезной азбуки составлено слово «книга».
Ребенок, не умеющий читать, рассыпал эти буквы и затем собрал в произвольном порядке. Найти вероятность р того, что у него снова получилось слово «книга».

2.69. Тот же вопрос, если было составлено слово «ананас».

2.70. Из полной колоды карт (52 листа, 4 масти) вынимается сразу
несколько карт. Сколько карт нужно вынуть для того, чтобы с вероятностью, большей чем 0,50, утверждать, что среди них будут карты од­ной и той же масти?

2.71. N человек случайным образом рассаживаются за круглым
столом (N > 2). Найти вероятность р того, что два фиксированных
лица А и В окажутся рядом.

2.72. Та же задача, но стол прямоугольный, и N человек рассаживаются случайно вдоль одной из его сторон.

2.73. Имеется М операторов и N перенумерованных приборов, ко­торые они могут обслуживать. Каждый оператор выбирает случайным
образом и с одинаковой вероятностью любой прибор, но с условием,
что ни один прибор не может обслуживаться больше, чем одним опера­тором. Найти вероятность того, что будут выбраны для обслужива­ния приборы с номерами 1, 2,..., М.

2.74. В ящике имеется К ТЭЗ, из них К₁ элементов 1-го типа,..., K_i элементов i -го типа,..., К_т элементов т -го типа; . Из ящика выбирают наугад k ТЭЗ. Найти вероятность того, что среди них будет k₁ ТЭЗ 1-го типа,..., k_i ТЭЗ i -го типа,..., k_m ТЭЗ т -го типа.

2.75. В отделение связи поступило 4 телеграммы; всего имеется
четыре канала связи. Телеграммы случайным образом распределяют­ся по каналам; каждая телеграмма с одной и той же вероятностью пе­редается по любому из четырех каналов. Найти вероятность события
А = {на один из каналов попадут три телеграммы, на другой — одна
телеграмма, а два оставшихся канала будут не загружены}.

2.76. М телеграмм случайным образом распределяются по N каналам связи (N > М).Найти вероятность события

А = {на каждый канал придется не больше одной телеграммы}.

Решить задачи 2.77. - 2.99., используя подходящие комбина­торные схемы.

2.77. Множество Е состоит из трех различных элементов:
Е = { а, b, с }.Выписать состав Ω во всех четырех опытах по вы­бору двух элементов из множества Е без возвращения и с возвращением, без упорядочивания и с упорядочиванием. Определить число элементов множества Ω(число различных выборок) в каждом из четырех случаев и сравнить результат с тем, который получается по соответствующей комбинаторной формуле.

2.78. Опыт состоит в случайном выборе одного элемента из
множества Е₁ = { а, b }и одного элемента из множества Е₂ = { а, b, с }. Перечислить состав множества Е = Е₁ * Е₂. Какова вероятность того, что выборка будет состоять из одинаковых элементов?

2.79. Из урны, содержащей шары с номерами 1, 2,..., п,
k раз вынимается шар и каждый раз возвращается обратно.
Найти вероятность того, что номера вынутых шаров образуют возрастающую последовательность.

2.80. Зенитная батарея, состоящая из n орудий, производит залп по группе, состоящей из m самолетов. Каждое из орудий выбирает себе цель наудачу независимо от остальных. При т > п найти вероятность того, что орудия выстрелят по различным самолетам.

2.81. Из урны, содержащей шары с номерами 1, 2,..., п, наудачу отбирается k шаров и номера вынутых шаров записываются
последовательно. Какова вероятность того, что на фиксированном
т -месте 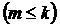окажется шар с номером т, если выбор осуществляется: а) без возвращения; б) с возвращением?

2.82. На тренировке детской спортивной школы по футболу
роли игроков распределяются случайным образом среди одиннадцати участников. Нужно отобрать одного вратаря, четырех за­
щитников, трех полузащитников и трех нападающих. Какова вероятность того, что два друга-участника Коля и Миша: а) будут
играть в нападении; б) получат разные роли, причем один из дру­зей будет играть в нападении, а другой — в защите?

2.83. В лотерее выпущено n билетов, из которых m выигрыш­ные. Куплено k билетов. Какова вероятность следующих событий:
А = {из k билетов хотя бы один выигрышный}, В = {из k билетов
ровно один выигрышный}, С = {из k билетов ровно k₁ выигрыш­ных}?

2.84. Какова вероятность р_п того, что в группе из n (n 365)
случайно отобранных студентов хотя бы у двоих окажется один и
тот же день рождения? Оценить значение р_п для п = 24 и п = 50.

2.85. На заводе работает 30000 рабочих и служащих. Показать, что на данном заводе обязательно найдутся хотя бы два человека с одинаковыми инициалами имени, отчества и фамилии.

2.86. Регистр калькулятора содержит 8 разрядов. Считая,
что появление любого числа на регистре равновероятно, опреде­лить вероятности следующих событий: А = {во всех разрядах
стоят нули}, В = {во всех разрядах стоят одни и те же цифры}.

2.87. (продолжение). В условиях предыдущей задачи найти
вероятности следующих событий: С = {регистр содержит ровно
две одинаковые цифры}, D = {регистр содержит ровно две пары
одинаковых цифр}.

2.88. (продолжение). В условиях задачи 2.86. найти вероятности событий: Е = {регистр содержит ровно три одинаковые
цифры}, F = {регистр содержит три и только три различные цифры}.

2.89. 7 яблок, 3 апельсина и 5 лимонов раскладываются случайным образом в три пакета, но так, чтобы в каждом было оди­наковое количество фруктов. Найти вероятности следующих событий: А = {в каждом из пакетов по одному апельсину}, В = {определенный пакет не содержит апельсинов}.

2.90. Из множества чисел Е = {1, 2,..., n } выбирается два
числа. Какова вероятность, что второе число больше первого, если
выбор осуществляется: а) без возвращения; б) с возвращением?

2.91. Из множества чисел Е = {1, 2,..., п }выбирается три
числа. Какова вероятность того, что второе число заключено между
первым и третьим, если выбор осуществляется: а) без возвращения; б) с возвращением?

2.92. Каждая из n палок случайным образом ломается на две
части — длинную и короткую. Затем 2 n полученных обломков
наудачу объединяются в п пар, каждая из которых образует новую
палку. Найти вероятности следующих событий: А = {все обломки
объединятся в первоначальном порядке}, В = {все длинные части
объединятся с короткими}.

2.93. Путем жеребьевки разыгрывается шесть подписных из­даний среди десяти участников.

Сколько различных распределений подписок возможно, если каждое очередное наименование разыгрывается между всеми участ­никами? Найти вероятность того, что первые шесть человек по­лучат каждый по одной подписке.

2.94. (продолжение). В условиях предыдущей задачи отве­тить на те же вопросы, если каждый участник, получивший под­писку, выбывает из игры.

2.95. Опыт состоит в том, что п различных предметов слу­чайным образом распределяются среди m человек (т < п), при­чем таким образом, что каждый может получить любое число пред­метов из имеющихся. Какова вероятность следующих событий: А = {все предметы достанутся одному из участников}, В = {опре­деленное лицо не получит ни одного предмета}.

2.96. (продолжение). В условиях эксперимента предыдущей задачи найти вероятности событий: С = {определенные т₁ лиц получат по одному предмету}, D = {определенные п₁ предметов достанутся одному из участников}.

2.97. В условиях эксперимента, описанного в задаче 2.50.,
найти вероятности следующих событий: Е = {автомобили разъедутся по улицам попарно}, F = {по определенной улице поедут два автомобиля}.

2.98. Условия эксперимента, описанного в задаче 2.50., из­менены следующим образом: на перекрестке запрещены разво­роты. Все остальные направления движения для любого из автомобилей равновероятны. Найти вероятности событий Е и F,определенных в предыдущей задаче.

2.99*. Из совокупности всех непустых подмножеств множе­ства Е = { e₁, е₂,..., е_п }по схеме выбора с возвращением отби­раются два подмножества Е₁ и Е₂. Какова вероятность того, что они пересекаются?