Теоретико-множественная семантика логики предикатов

Интерпретация выражений языка логики предикатов предполагает наличие непустой предметной области, функции приписывания значений индивидным константам, функциональным и предикаторным символам, сложным выражениям, а также наличие функций, соотнесенных с предметной областью, которые приписываю значения свободным индивидным переменным.

Пусть предметная область, или универсум рассуждений, - непустое множество D, функция приписывания значений индивидным константам, функциональным и предикаторным символам, 1 а также сложным выражениям - ||. Множество (D, ||) называется моделью. - функции приписывания значений свободным индивидным переменным формулы, или распределения значений по свободным индивидным переменным формулы, соотнесенные с предметной областью модели (D, ||).

Значения приписываются следующим образом.

Если - индивидная константа, то . Выражение читается: значение индивидной константы в данной модели есть некоторый предмет из области D.

Если - свободная индивидная переменная некоторой формулы, то . Функция распределения значений по свободным переменным формулы приписывает свободной переменной элемент из D.

Если - n-местный предметный функтор, то ему в качестве значения функция || приписывает n-местную функцию, т.е. есть функция, отображающая 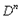в D.

Если 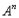- n-местный предикатор, то 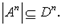То есть n-местному предикаторному символу приписывается в качестве значения некоторое множество n-ок предметов. Если n = 1, то это множество предметов, составляющих объем имени 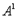, а если, например, n = 2, то это множество пар предметов, составляющих объем соответствующего имени. Пусть 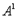- предикатор «человек», а D - множество живых существ. Тогда есть множество всех людей. Пусть есть предикатор «больший, чем», а D - множество целых положительных чисел, тогда - множество всех пар целых положительных чисел таких, что первое число больше второго.

Интерпретация сложных выражений.

Если - n-местный предметный функтор, а 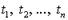- термы, то 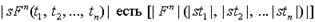то есть объект из области D, который является результатом применения функции к n-ке предметов Если терм 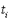не содержит свободных переменных, то 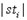есть 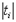, а если терм представляет собой индивидную переменную, то 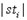есть 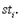Выражение 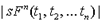читается: значение при распределении s.

Пример. Терм D - множество натуральных чисел, |а| есть 2, sx есть 3, есть +. Тогда 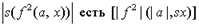и есть +(2, 3), и есть 6.

Если 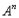- n-местный предикатор, а 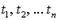, - термы, то 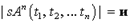, если, и только если,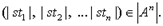

Пример. Формула 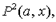D - множество натуральных чисел, |а| есть 2, sx есть 3, есть {(1, 0), (2, 1), (2, 0), (3, 0),...}, т.е. есть отношение «больше». Тогда 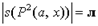, так как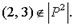

Далее вместо |sA| будем писать 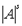. Если А не имеет свободных вхождений переменных, то - |А|.

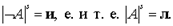
Пояснение. Вместо «е. и т. е.» будем писать «». - знак метаязыковой эквивалентности. Поскольку формула классической логики предикатов обязательно принимает одно, и только одно, значение из области {и, л}, при отрицании выражений соответственно получаем Тогда

* Знаки метаязыка, по начертанию совпадающие со знаками объектного языка (в данном случае со знаками языка логики предикатов, кроме запятой), набираются полужирным шрифтом.

Пояснение. Распределение 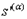является -альтернативным относительно s, е. и т.е. приписывает всем свободным переменным формулы или множеству формул, или бесконечному множеству индивидных переменных, кроме, возможно, переменной , те же значения, что и s, иначе, - е. и т. е. 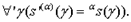(Обозначения - -альтернативное распределение относительно s; 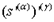- -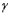альтернативное распределение относительно ; и т.д.);

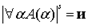, е. и т.е. для любого распределения, являющегося -альтернативным относительно s, 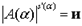, т.е. 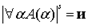, е. и т.е. (Следствия: , в случае если формула не имеет вхождений свободных переменных).

Замечание: если из контекста ясно, относительно какой переменной распределение является альтернативным, то указание на переменную будем опускать, т.е., например, вместо 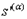будем писать s'.

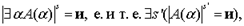где s' - то же, что и в предшествующем случае. (Следствие: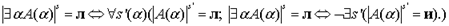

Определения. Формула А общезначима в модели (D, ||), е. и т. е, она истинна в этой модели при любом распределении значений по свободным переменным, соотнесенным с предметной областью этой модели. Формула (логически) общезначима (обозначение: |=В), е. и т.е. она общезначима в каждой модели.

Конечное множество формул совместимо по истинности, е. и т.е. существуют модель (D, ||) и распределение s, соотнесенное с предметной областью этой модели, такие, что все формулы из этого множества истинны в этой модели при этом распределении.

Множество формул совместимо по ложности, е. и т.е. существуют модель (D, ||) и распределение s, соотнесенное с предметно областью этой модели, такие, что все формула из этого множества ложны в этой модели при этом распределении.

Из множества формул логически следует формула В (обозначение: 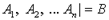), е. и т.е. не существует модели и распределения, соотнесенного с предметной областью этой модели, таких, что при этом распределении в этой модели формулы 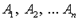истинны, а В ложна.

Другие отношения (производные) легко определяются на основе этих (основных) отношений.

Примеры. (1) Является ли общезначимой формула

Будем рассуждать от противного. Допустим, что она не является общезначимой, т.е. существует модель (D, ||), в которой эта формула принимает значение л.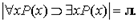

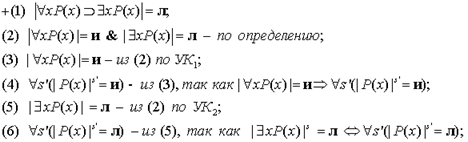
(7) |Р(а)| = и - из (4), так как если для любого s' верно 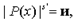, то это верно для произвольного объекта, который обозначим как а;

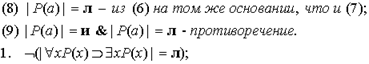
6.2.3. Семантические таблицы

При построении семантических таблиц для формул языка логики предикатов используются правила редукции, приведенные при описании семантических таблиц для формул логики высказываний. Эти правила теперь применяются для формул логики предикатов. Сохраняются понятия подтаблицы и таблицы, замкнутой подтаблицы и таблицы, а также понятия отношения логического следования, совместимости и несовместимости формул (и соответствующих им суждений) по истинности и ложности. Добавляются новые правила редукции:

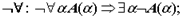
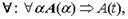где A(t) - результат правильной подстановки терма t вместо в А(). Эвристический совет: в качестве t нужно взять терм, который входит в какую-то из формул подтаблицы свободно, т.е. не имеет индивидных переменных или, если имеет, то они не связаны кванторами. Если такого терма нет, то вводится произвольная индивидная константа.

 

- новая индивидная константа.

Пример 1. Некоторые литературно-художественные произведения - философские. Все философские произведения - мировоззренческие. Следовательно, некоторые мировоззренческие произведения - литературно-художественные.

Посылки этого рассуждения на языке логики предикатов выражаются формулами: а заключение - формулой Следует ли в этом рассуждении заключение из посылок?

Будем, как это делалось при построении семантических таблиц для формул логики высказываний, рассуждать от противного, т.е. допустим, что посылки истинны, а заключение ложно. Помещаем в таблицу формулы

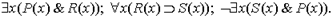
Попытаемся получить противоречие из этого допущения. Если таблица замкнется, то придется признать допущение неверным, а исходное рассуждение правильным.

Рассмотрим формулу 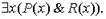Если это утверждение истинно, то имеется какой-то объект а, для которого верно применяя правило 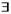. Поэтому к исходному множеству добавляем формулу Напишем ее под номером 1, отметив тем самым первый шаг продолжения построения семантической таблицы:

Рассмотрим (на втором этапе) формулу Если соответствующее этой формуле утверждение является истинным, то для любого предмета х верно R(x) 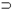S(x), а значит, это верно и для а. Применяем правило 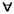. Под номером 2 напишем R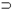(a) S(a).

Далее (на третьем шаге) рассмотрим формулу Применяем правило . Под номером 3 пишем формулу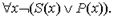

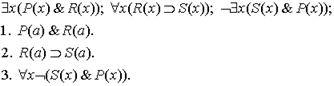
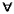К формуле применяем правило . Поскольку наша цель - получить противоречие, подставляем вместо х ту индивидную константу (тот терм), которая входит в какую-то из формул таблицы, т.е. а.

К 4 применяем правило .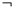

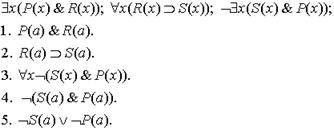
К 1 применяем правило.

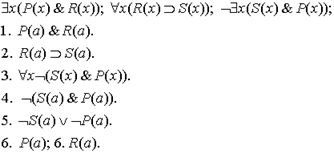
Применяем правило 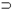к формуле 2. Образуем подтаблицы. В одну помещаем формулу 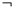R(a), в другую - S(a).

Одна из подтаблиц замкнулась, так как в ней имеются формулы R(a) и 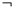R(a).

Применяем правило к формуле 5. Из оставшейся незамкнутой подтаблицы образуем две новые подтаблицы.

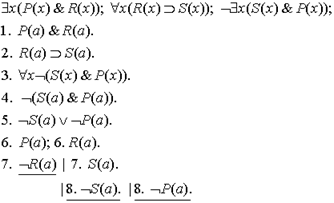
Все подтаблицы замкнуты. Замкнута таблица. Следовательно, исследуемое рассуждение является правильным.

Эвристические советы:

1) следует сначала применить все правила редукции, которые не требуют образования подтаблиц;

2) при применении правил 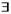и 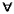сначала целесообразно применять правила 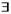, а затем правила .

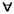Возможны три результата построения семантической таблицы: таблица оказывается замкнутой (в этом случае исследуемое рассуждение является правильным, а если анализировалось отдельное высказывание - это высказывание является логически истинным все возможные правила применены, а таблица не замкнулась (рассуждение является неправильным, а если анализировалось отдельное высказывание - это высказывание не является логически истинным); процесс построения таблицы оказывается бесконечны (в этом случае задача не решена).

Пример 2 (пример таблицы, подтверждающий существование третьей возможности). Следует ли из формулы формула ?

6.2.4.

Исчисление предикатов. Аксиоматическое построение

Система со схемами аксиом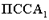

Язык содержит те же символы, что и язык предикатной СНВ, кроме знака материальной эквивалентности.

Схемы аксиом

Схемы аксиом, совпадающие со схемами аксиом исчисления высказываний .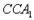

1. 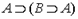- утверждение консеквента.

2. 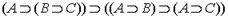- самодистрибутивность материальной импликации.

3. - ВК (введение конъюнкции).

4. 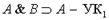(удаление конъюнкции первое).

5. (удаление конъюнкции второе).

6. 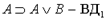(введение дизъюнкции первое).

7. (введение дизъюнкции второе).

8. - ПКД (простая конструктивная дилемма).

9. - СА (сведение к абсурду).

10. - УДО (удаление двойного отрицания).

Дополнительные схемы аксиом:

1. А(t) - результат правильной подстановки терма t вместо в А().

2. A(t) - результат правильной подстановки терма t вместо в А().

3. - введение 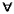в консеквент, В не имеет свободных вхождений .

4. - введение в антецедент, В не имеет свободных вхождений .

Правила вывода:

1. МП (modus ponens)

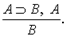
2. Правило обобщения

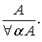
Доказательством называется непустая конечная последовательность формул, в которой каждая формула есть или аксиома, или формула, полученная из предшествующих формул последовательности по одному из правил вывода. Доказательство называется доказательством последней формулы последовательности. Формула, для которой имеется доказательство, называется теоремой. Факт наличия доказательства формулы В выражается так: |-В.

Выводом из множества гипотез (посылок, допущений) Г называется непустая конечная последовательность формул, в которой каждая формула есть или аксиома, или гипотеза из Г, или формула, полученная из предшествующих формул последовательности по одному из правил вывода. Вывод является выводом последней формулы этой последовательности из множества гипотез Г. Факт наличия вывода формулы В из множества гипотез Г записывается так: Г |- В. Замечание: переменная , на которую навешивается квантор общности при применении правила обобщения, не должна иметь свободных вхождений в гипотезы.

Свойства исчисления предикатов 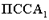. (Это исчисление эквивалентно предикатной СНВ по множеству доказуемых формул.)

1.Исчисление семантически непротиворечиво, т.е.

Аксиомы, задаваемые схемами, совпадающими со схемами аксиом исчисления высказываний 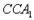являются общезначимыми формулами. Для убеждения в этом достаточно построить таблицы истинноcти для этих схем.

Общезначимость аксиом, задаваемых дополнительными схемами, можно установить семантически.

Правило обобщения сохраняет свойство общезначимости формул. Возможны два случая его применения.

Первый. Формула А не имеет свободных вхождений переменной .

Тогда есть А. Очевидно, что в этом случае свойство общезначимости сохраняется.

Второй. Формула А имеет свободные вхождения переменной . Тогда для любой модели и для любого распределения Это же условие является условием общезначимости формулы .

Правило МП тоже сохраняет свойство общезначимости формул.

2. Исчисление предикатов непротиворечиво относительно oтрицания.

3. Проблема разрешимости для исчисления предикатов решается отрицательно.

4. Исчисление предикатов не является синтаксически полным т.е. добавление в качестве аксиомы не доказуемой в исчислении формулы не обязательно делает исчисление противоречивым. Это свойство исчисления предикатов позволяет строить его расширения.

Расширения исчисления предикатов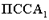

Исчисление предикатов с равенством

Построенные исчисления предикатов являются узкими исчислениями предикатов. Исчисления, к которым добавляются в качестве аксиом постулаты какой-либо теории, называются прикладными. Покажем, как может расширяться узкое исчисление предикатов. Описываемое ниже исчисление, хотя оно и содержит дополнительные аксиомы, не выводимые в узком исчислении, все еще остается логическим, поскольку отношение равенства считается логическим. (Если же добавляются нелогические постулаты, то исчисление напивается прикладной теорией.)

Для получения исчисления предикатов с равенством добавим к аксиомам еще две аксиомы с двухместным предикатором . Для удобства заменим его знаком равенства.

Дополнительные схемы аксиом.

и - индивидные переменные, A() - результат замены некоторых (возможно всех) свободных вхождений переменной на в A(). При этом после замены вхождения переменной не должны оказаться в области действия какого-либо из кванторов по этой переменной.

Формальная арифметика

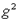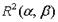Язык содержит только одну предикаторную константу (равенство), одну индивидную константу а (число 0), три предметно-функциональные константы: (следующий за), (сложение), (умножение). Вместо будем писать 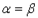, вместо а - 0, вместо ( и - индивидные переменные.)

Схемы аксиом и правила вывода чистого исчисления предикатов первого порядка сохраняются.

Дополнительные схемы аксиом:

9) произвольная формула; - принцип математической индукции.

Исчисление не является семантически полным.

Оно включает в себя исчисление предикатов с равенством. (Специальные схемы аксиом равенства в нем доказуемы.)