При точечной оценке параметра l сигнала s (t,l) произвести оценку, - это значит каждой из возможных реализаций x (t) поставить в соответствие некоторую величину γ = γ[x(t)] из интервала возможных значений оцениваемого параметра L, называемую точечной оценкой.
Из-за случайного характера точечной оценки параметра сигнала на фоне помех ее характеризуют условной плотностью помех вероятности w (γ /l). Это наиболее общая и полная характеристика оценки. Вид этой плотности вероятности определяет качество построения оценки n, cледовательно, определяет все свойства оценки.
Плотность вероятности ω (γ /l) при заданном правиле оценки γ =γ [ x (t) ] может быть получена из плотности вероятности реализации x (t) с помощью правила преобразования плотностей вероятности.
Для этого рассмотрим дискретное представление X (x1, x2, …,xν) и введем новы переменные ξ1 = x1, ξ2 =x2…ξγ-1 = xγ-1, ξν=γ=γ(x1,x2,…,xγ).
Будем полагать, что существует обратное однозначное преобразование xγ =ψ(ξ1…ξν).
|
|
|
Тогда якобиан преобразования от переменных (x1,x2…xν) к новым переменным (ξ1,ξ2…ξν) равен
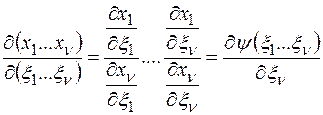 ,
,
а многогранная плотность вероятности случайных величин (ξ1,ξ2,…ξν) имеет вид
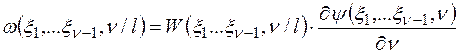
Отсюда искомая плотность вероятности ω(γ/ℓ) равна
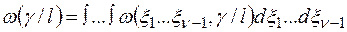
Непосредственное нахождение плотности вероятности ω(γ/ℓ) во многих прикладных задачах весьма затруднительно. Поэтому, если есть основания предполагать, что плотность вероятности ω(γ/ℓ) унимодальна и близка к симметричной, то в качестве характеристик сгруппированности оценки γ относительно значения ℓ используют широко распространенные понятия смещения рассеяния и дисперсии оценки, которые могут быть вычислены без непосредственного определения плотности вероятности ω(γ/ℓ).
Смещение, рассеяние и дисперсия определяются из следующих выражений:
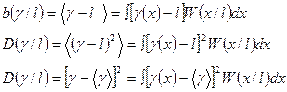
Угловые скобки 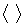 означают усреднение случайной величины или функции по ее значениям (или реализациям), что тождественно соотношению
означают усреднение случайной величины или функции по ее значениям (или реализациям), что тождественно соотношению
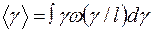
Если оценка γ формируется без учета определенной плотности Wpr (ℓ), то оценки и ее характеристики в D, D называются условными. Оценка, формируемая с учетом априорного распределения, называется безусловной. Безусловные характеристики оценки получаем, усредняя условные по возможным значениям переменной l с априорным распределением Wpr (ℓ):
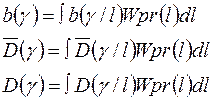
Оценка параметра сигнала, для которой условное смещение равно нулю, называется условно не смещенной, т. е. в этом случае среднее значение оценки совпадает с истинным значением оцениваемого параметра 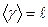 . Если равно нулю безусловное смещение, то оценка будет безусловно несмещенной, т.е.
. Если равно нулю безусловное смещение, то оценка будет безусловно несмещенной, т.е. 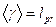 , где lpr - априорное среднее значение параметра.
, где lpr - априорное среднее значение параметра.
|
|
|
При совместной оценке нескольких параметров, например, при оценке векторного параметра l с составляющими l1, l2, …,lр помимо введенных оценок требуется знать статическую связь между ошибками оценки Для этой цели используются коэффициенты и функции взаимной корреляции оценок.
Если обозначить оценки параметров l1, l2, …, lр соответственно через γ1, γ2,…γр,то условные функции взаимной корреляции оценок параметров li и lj оцениваются как
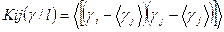
Из этих величин составляется матрица ошибок, причем величины по диагонали матрицы являются условными дисперсиями оценок.
Свойства точечных оценок:
1) Естественно пытаться построить такую точечную оценку γ, чтобы условная плотность вероятности ω (γ/l) была как можно более тесно сгруппирована вокруг значения l,
2) Весьма желательно, чтобы при длительном времени наблюдения Т → ∞ или в отсутствие помех (отношение сигнал/помеха неограниченно возрастает) оценка совпадала с истинным значением оцениваемого параметра. В этом случае говорят, что оценка состоятельная.
3) Оценка д. б.несмещенной или, в крайнем случае, асимптотически несмещенной т.е. несмещенной при Т → ∞ или при неограниченном увеличении отношения сигнал/шум.
4) Оценка должна характеризоваться минимальными значениями рассеяния или дисперсии (при нулевом или постоянном смещении)
5) Оценка должна обладать свойствами достаточности (являться достаточной статистикой). Статистика (или функция наблюдаемых данных) является достаточной, если все суждения об оцениваемом параметре могут быть вынесены на основании этой статистики без дополнительного обращения к реализации принятых данных. Очевидно, что апостериорная плотность вероятности всегда является достаточной статистикой.
Условие достаточности оценки можно сформулировать в терминах функции правдоподобия: необходимым и достаточным условием достаточности оценки является представления функции правдоподобия двух функций
W (x / l) = h [ x (t) ] q (γ/l)
где h [ x (t) ] -некоторая произвольная функция от x (t), не зависящая от оцениваемого параметра l. Так как параметр l не входит в функцию h, то ее нельзя использовать для получения информации об l. Множитель q (γ/l) зависит от x (t), только через оценку γ [x (t) ], так что в γ [ x (t) ] должна содержаться вся информация об оцениваемом параметре l.
Существует важное понятие эффективной оценки.
Применительно к смещенным оценкам параметра сигнала оценка lЕ называется эффективной, если среднее значение квадрата отклонения оценки от истинного значения оцениваемого параметра l не превышает среднее значение квадрата отклонения любой другой оценки γ, т. е. выполняется неравенство

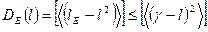
Для несмещенной оценки [ b (γ/l) = 0 ] рассеяние оценки совпадает с ее дисперсией D (γ/l) = D (γ/l) и, следовательно, эффективная несмещенная оценка определяется как оценка с минимальной дисперсией.
Лекция №23
ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ СТАТИСТИЧЕСКИХ ОЦЕНОК
В теории статистических оценок различают два вида правил выбора решения: неслучайные (нерандомизированные) и случайные (рандомизированные).
Для неслучайного правила выбора решения (оценки) по каждой конкретной реализации принятых данных x(t) принимается одно, вполне определённое решение, т.е. между принятой реализацией и выносимым решением существует детерминированная зависимость. Тем не менее в силу случайного характера наблюдаемых данных решения при оценке являются случайными величинами.
Для случайного правила выбора решения по каждой конкретной реализации x(t) принимается не одно какое–нибудь решение, а задаётся вероятность того или иного решения, т.е. зависимость между принятой реализацией и выносимым решением носит вероятный характер.
|
|
|
Наиболее часто применяются нерандомизированные (неслучайные) правила выбора решения.
Из-за случайного характера наблюдаемой реализации при любом правиле выбора решения неизбежны ошибки в том смысле, что принятое решение g (оценка) совпадает с истинным значением параметра ℓ. Очевидно, при различных правилах выбора решения, ошибки различной величины будут появляться с различной вероятностью. При этом в зависимости от цели получения оценки, последствия появления ошибок могут быть различными. Поскольку всегда имеется, отличная от нуля вероятность ошибки, то необходимо тем или иным образом охарактеризовать качество различных оценок. С этой целью в теории введено понятие функции потерь.
Эта функция каждой комбинации из решения g и параметра ℓ приписывает определённую потерю C(g, ℓ). Обычно потери выбирают неотрицательными, а правильными решениям приписывают нулевые потери.
Физический смысл ФП состоит в том, что каждой возможной ошибке приписывается определённый неотрицательный вес. При этом в зависимости от целей, для которых находится оценка, наименее желательным ошибкам приписываются наибольшие веса. Выбор той или иной ФП производится в зависимости, от конкретной специфики задачи, для которой находится оценка, и выходит за рамки теории статистических решений.
Не существует общего формального правила выбора ФП и он в той или иной степени является субъективным.
Наиболее часто используются следующие ФП:
1) Простая
С (g, ℓ) = Со – σ (γ - ℓ), Со>0
σ (r) – дельта – функция Дирака
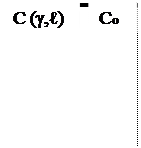 | |||
 |
 | |||
 | |||
2) линейная по модулю.
С (γ, ℓ) =|γ-ℓ|
 |
 | |||
 | |||
3) квадратичная С (γ, ℓ) = 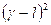
 |
 |
4)
 |  | ||||||
 |  | ||||||
прямоугольная C (γ,ℓ)
 |  |  | |||
5) экспоненциальная
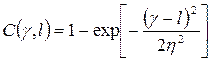
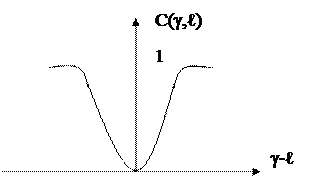
|
|
|
Все эти ФП являются симметричными. При этом отклонения оценки относительно истинного значения в ту и другую стороны одинаково нежелательны.
 |
Существуют задачи, в которых отношение наблюдается к знаку ошибки разное. Для таких ситуаций ФП будут несимметричными. Примером такой ФП может служить так называемая информационная ФП вида
Здесь W(ℓ/γ) – условная плотность вероятности параметра ℓ, если принята оценка (решение) γ. Функцию потерь вида (*) можно интерпретировать как меру неопределённости относительно параметра ℓ, если известна оценка ℓ.
В силу случайного характера оценок γ и параметра ℓ потери при любом правиле выбора решения являются случайными и не могут быть использованы для характеристики качества оценки (правила выбора решения).
Для характеристики качества оценки можно принять среднее значение ФП, которое будет учитывать все возможные типы поведения системы оценки, все виды ошибок и относительную частоту их появления.
Среднее значение (условное или безусловное) функции потерь называются риском ( условным или безусловным).
Условный риск получается путём усреднения ФП по возможным значениям многомерной выборки наблюдаемых данных, характеризуемой условной плотностью вероятности W (x/ℓ)
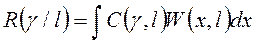 (7)
(7)
Из этого выражения и определения ФП следует, что более предпочтительными оценками будут те оценки, при которых условный риск минимален. Однако при парных значениях оцениваемого параметра ℓ условный риск будет иметь различные значения. Поэтому м.б. различными наиболее предпочтительные оценки.
Значит, если известно априорное распределение значений оцениваемого параметра, то наилучшее правило выбора решения (оценку) целесообразно искать исходя из условия минимума безусловного среднего риска:
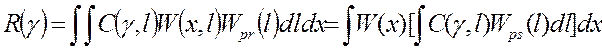 (8)
(8)
где W(x) – плотность вероятности выборки наблюдаемых данных.
Оценки, получаемые по критерию минимального, условного или безусловного (среднего) риска называются соответственно условными и безусловными байесовскими оценками. Под байесовской оценкой γm параметра ℓ будем понимать оценку, обеспечивающую минимальное значение безусловного среднего риска (8) при заданной ФП С(γ,ℓ).
Минимальное значение безусловного среднего риска соответствующее байесовской оценке, называют байесовским риском
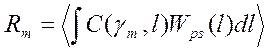 (9)
(9)
Здесь условие выполняется по выборкам наблюдаемых данных.
Безусловный средний риск (8) может быть вычислен для любого заданного правила выбора решения, причём в силу определения байесовской оценки всегда выполняется условие
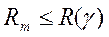 (10)
(10)
Вычислим средний риск (8) для различных оценок и сравнивая эти риски между собой байесовским риском, можно судить, насколько одна оценка лучше другой и насколько какая – либо оценка близка к оптимальной (байесовской) оценке.
Так как сам риск (условный или безусловный имеет различный физический смысл в зависимости от вида и физической интерпретации функции потерь С(γ,ℓ), то смысл критерия оптимальности зависит также от вида функции потерь.
Поскольку плотность вероятности W(x) есть неотрицательная функция, то минимизация выражения (8) по γ сводится к минимизации функции
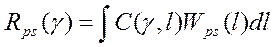
Называется апостериорным риском, при фиксированной выборке (реализации) наблюдаемых данных. Если апостериорный риск дифференцируем по γ, то байесовская оценка γm м.б. найдена как решение уравнения
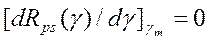
При этом берётся корень уравнения, обеспечивающий глобальный минимум (минимум миниморум) апостериорного риска.
Критерий минимума среднего риска основан на использовании полной априорной информации об оцениваемом параметре, т.е. даёт ответ на вопрос, каким образом надо использовать всю априорную информацию, чтобы получить наилучшую оценку. Однако имеет место отсутствие полной априорной информации в ряде прикладных задач. В этом случае (если известно априорное распределение оцениваемого параметра) отыскивают байесовские оценки, инвариантные по отношению к достаточно широкому классу распределений.
Если в качестве априорного распределения оцениваемого параметра взято наименее предпочтительное распределение, при котором байесовской риск будет максимален, то получаемая оценка параметра сигнала называется минимаксной. Минимаксная оценка даёт оптимальное решение только для самого наихудшего случая и определяет верхнюю границу байесовского риска, которую называют минимаксным риском. Хотя минимаксная оценка может приводить к большим потерям, чем другая оценка, она м.б. полезной, если желательно застраховаться от потерь за счёт оценивания в наиболее неблагоприятных априорных условиях.
Минимаксная оценка может быть найдена следующим образом. Для произвольного априорного распределения в соответствии о заданной функции потерь ищется байесовская оценка 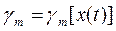 . Затем подбирается такое априорное распределение оцениваемого параметра, при котором минимальное значение среднего риска (байесовский риск) достигает максимума. Байесовская оценка при таком априорном распределении будет максимальной. В большем числе прикладных задач наиболее предпочтительным распределением является равномерное.
. Затем подбирается такое априорное распределение оцениваемого параметра, при котором минимальное значение среднего риска (байесовский риск) достигает максимума. Байесовская оценка при таком априорном распределении будет максимальной. В большем числе прикладных задач наиболее предпочтительным распределением является равномерное.
Байссовские оценки для различных функций потерь.
1 Простая ФП.
Подставляя простую ФП в выражение для апостериорного риска 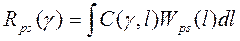 и используя фильтрующее свойство d - функции
и используя фильтрующее свойство d - функции
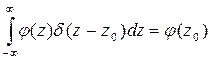
получим
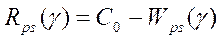
Апостериорный риск, а согласно и средний риск R(g), будут минимальны, если апостериорная плотность вероятности Wps(g) для данной оценки принимает наибольшее значение из всех возможных значений. Это означает, что в качестве взято наиболее вероятное значение gm, при котором выполняется условие
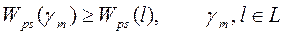
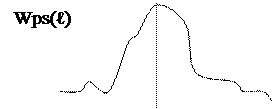 |
 | |||
 | |||
Байесовская оценка при простой функции потерь минимизирует вероятность неправильного решения. При этом всем ошибкам приписывается одинаковый вес Со, т.е. предполагается, что все ошибки нежелательны независимо от их величин.
2 Линейная по модулю ФП.
Апостериорный риск для данной ФП определяется из выражения 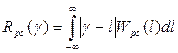 .
.
Освободимся от модуля в подынтегральном выражении, для чего интервал интегрирования (-∞,∞) разобьем на два равных интервала: -∞<ℓ<g и g<ℓ<∞, в каждом из которых можно определить знак модуля. Тогда
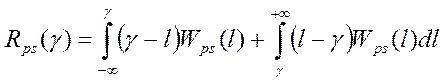
Из условия экстремума функции Rps(g) получаем уравнение для оценки gm
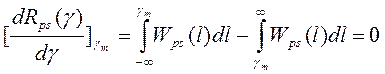
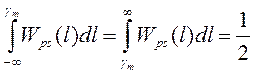
При этом
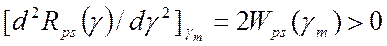 ,
,
т.е.gm соответствует минимуму Rps(g).
Из последнего выражения видно, что в качестве оценки параметра берется то его значение, при котором площади под кривой апостериорной плотности вероятности слева и справа равны, т.е. байесовская оценка представляет медиану апостериорного распределения.

gm
Анализируя выражение байесовского риска при линейной ФП
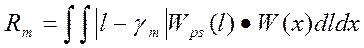
видим, что байесовский риск равен минимальному среднему значению модуля отклонения медианы апостериорного распределения от истинного значения оцениваемого параметра.
3 Квадратичная ФП
Для квадратичной ФП имеем:
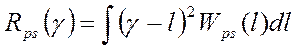
Из условия экстремума функции Rps(γ) получаем выражение для оценки
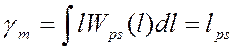
 |
Следовательно, в качестве оценки параметра ℓ при квадратичной ФП следует брать среднее значение апостериорного распределения (центр тяжести апостериорного распределения) ℓps.
Величина Rps(γ) характеризует минимальное мгновенное значение квадрата ошибки оценки параметра сигнала. Поскольку Rps(γ) зависит от конкретного вида реализации смеси сигнала и помехи x(t), мгновенное значение квадрата ошибки является случайным. Байесовский риск при квадратичной ФП совпадает с рассеянием оценки 

и равен
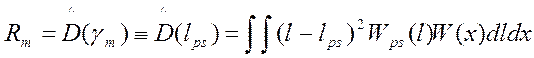
Байесовская оценка при квадратичной ФП обеспечивает минимальное значение рассеяния оценки относительно истинного значения оцениваемого параметра среди всех возможных оценок параметров сигнала.
4 Квадратичная ФП.
Для прямоугольной ФП характерно, что все мгновенные ошибки, которые по модулю меньше заданного значения η, одинаково неопасны для наблюдателя и с его точки зрения не приводят к какому – либо ухудшению качества оценки параметра. Ошибки, мгновенные значения которых по модулю превышают значение η, одинаково нежелательны и всем им приписываются одинаковый вес.
Разобьем интервал интегрирования на три подынтервала -∞<ℓ<γ-η, γ-η≤ℓ≤γ+η, γ+η < ℓ < ∞, тогда
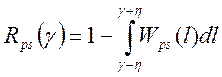
Из этого выражения видно, что в качестве байесовской оценки при прямоугольной ФП надо выбирать значение γ = γm, для которого вероятность выполнения неравенства |γ-ℓ| ≤ η максимальна.
Уравнение для оценки γm находим из условия экстремума апостериорного риска Rps(γ)
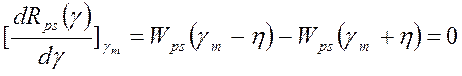
Или 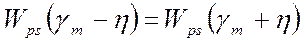
Последнее уравнение показывает, что в качестве байесовской оценки параметра сигнала необходимо взять то значение параметра γm, при котором значения апостериорной плотности вероятности, соответствующие параметрам, отстоящим от оценки слева и справа на величину η равны между собой.
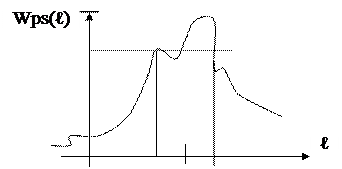
(γm-h) γm (γm+h)
Байесовский риск для прямоугольной ФП равен
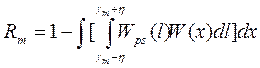
Байесовский риск определяет минимальную среднюю вероятность неправильного решения по данному критерию.
Лекция №24
 2014-01-31
2014-01-31 726
726








