Элементарные динамические звенья САУ

1.3.1 Особенности классификации звеньев САУ Основная задача теории автоматического управления ТАУ -разработать методы, с помощью которых можно было бы находить или оценивать показатели качества динамических процессов в САУ. Другими словами, рассматриваются не все физические свойства элементов системы, а только те, которые влияют, связаны с видом динамического процесса. Не рассматриваются конструктивное ис­полнение элемента, его габаритные размеры, способ подведения

энергии, особенности дизайна, номенклатура используемых мате­риалов и т.д. Однако, важными будут такие, например, параметры, как масса, момент инерции, теплоемкость, сочетания RC, LC и т.д., напрямую определяющие вид динамического процесса. Особеннос­ти физического исполнения элемента важны только в той степени, в которой они будут влиять на его динамические показатели. Рас­сматривается, таким образом, только одно выделенное свойство эле­мента - характер его динамического процесса. Это позволяет свести рассмотрение физического элемента к его динамической модели в виде математической модели. Решение модели, т.е. дифференциаль­ного уравнения, описывающего поведение элемента, дает динами­ческий процесс, подлежащий качественной оценке.

В основу классификации элементов САУ положены не осо­бенности конструктивного выполнения или особенности их функ­ционального назначения (объект управления, элемент сравнения, регулирующий орган и т.д.), а тип математической модели, т.е. мате­матические уравнения связи между выходной и входной переменны­ми элемента. Причем эта связь может быть задана, как в виде диффе­ренциального уравнения, так и в другой трансформированной форме, например с помощью передаточных функций (ПФ). Дифференциаль­ное уравнение даёт исчерпывающую информацию о свойствах звена. Решив его, при том или ином заданном законе входной величины, по­лучаем реакцию, по виду которой оцениваем свойства элемента.

Введение понятия передаточной функции позволяет получить связь между выходной и входной величинами в операторной форме и при этом воспользоваться некоторыми свойствами передаточной функции, позволяющими существенно упростить математическое представление системы и воспользоваться некоторыми их свойства­ми. Для объяснения понятия ПФ рассмотрим некоторые свойства преобразования Лапласа.

1.3.2 Некоторые свойства преобразования Лапласа Решение моделей динамических звеньев САУ дает измене­ние переменных во временной плоскости. Мы имеем дело с функ­циями X(t). Однако, с помощью преобразования Лапласа их можно трансформировать в функции [Х(р)] с другим аргументом р и новы­ми свойствами.

Преобразование Лапласа есть частный случай соответствия типа: одной функции ставится в соответствие другая функция. Обе функции связаны между собой определённой зависимостью. Соот­ветствие напоминает зеркало, отображающее различным образом, в зависимости от формы, находящийся перед ней объект. Вид отобра­жения (соответствия) может быть выбран произвольным образом, в зависимости от решаемой задачи. Можно, например, искать со­ответствие между совокупностью чисел, смысл которого сводится к тому, как по выбранному числу у из области Y найти число х из области X. Такая связь может быть задана аналитически, в виде таб­лицы, графика, правила и т.д.

Аналогично может быть установлено соответствие между группами функций (рис. 3.1 а), например, в виде:

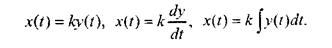
В качестве соответствия между функциями x(t) и х(р) (рис.3.1 б) может быть использован интеграл Лапласа:

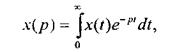
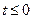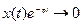при соблюдении условий: x(t) = 0 при и при t.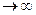

В САУ исследуются не абсолютные изменения переменных, а их отклонения от установившихся значений. Следовательно, x(t) - класс функций, описывающих отклонения переменных в САУ и для них выполняется оба условия преобразования Лапласа: первое - так как до приложения возмущения изменения переменных не происхо­дит, второе - так как с течением времени любое отклонение в рабо­тоспособной системе стремится к нулю.

Это условия существования интеграла Лапласа. Получим, в качестве примера изображения простейших функций но Лапласу.

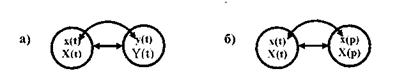
Рис. 3.1. Виды отображения функций

Так, если дана единичная функция x(t) = 1, то

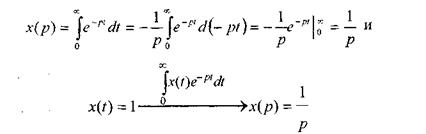
Для экспоненциальной функции x(t) = e^-αt изображение по

Лапласу будет иметь вид:

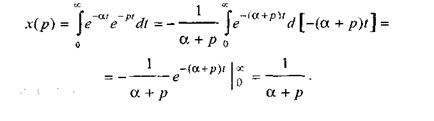
Окончательно:

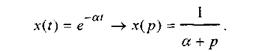
Полученные функции не сложнее исходных. Функция x(t) называется оригиналом, а х(р) - ее изображением. Условно прямое и обратное преобразование Лапласа можно представить в виде:

L[x(t)]=x(p),L^-1<[x(p)]=x(t).

При этом существует однозначная связь между оригиналом и изображением, и наоборот, оригиналу соответствует только единс­твенное изображение функции. Рассмотрим некоторые свойства преобразования Лапласа.

Изображение дифференциала функции. Пусть функции x(t) соответствует изображение х(р): x(t)—> х(р)- Необходимо найти изображение ее производной x(t):

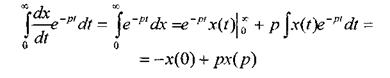
Таким образом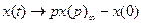

При нулевых начальных условиях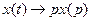

Для изображения производной n-го порядка: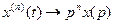

Таким образом, изображение производной функции есть изоб­ражение самой функции, умноженное на оператор p в степени n, где п - порядок дифференцирования.

Элементарным динамическим звеном (ЭДЗ) называется мате­матическая модель элемента в виде дифференциального уравнения, не подлежащего дальнейшему упрощению.

1.3.3 Инерционное апериодическое звено первого порядка

Такое звено описывается дифференциальным уравнением первого порядка, связывающего входную и выходную величины:

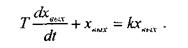
Примером такого звена кроме термопары, электродвигателя постоянного тока, RL-цепочки, может служить пассивная RC - цепочка (рис. 3.2 г).

Используя основные законы описания электрических цепей получим математическая модель апериодического звена в диффе­ренциальной форме:

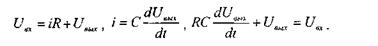
Получим связь между входной и выходной величинами звена в форме преобразования Лапласа:

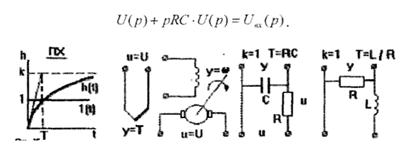
Рис. 3.2. Примеры апериодических звеньев

Отношение выходной величины к входной дает оператор вида:

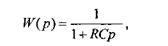
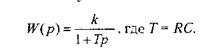который называется передаточной функцией (ПФ). Таким образом ПФ апериодическогозвена будет:

Инерционный характер процесса, т.е. немгновенность вос­произведения входной величины, определяется в этих звеньях од­нонаправленностью преобразования входного потока энергии, т.е. растянутым во времени аккумулированием энергетического пото­ка. Это вызвано таким основным физическим свойством данных элементов, как инерционность в виде массы, момента инерции, со­четания RC, LC. Инерционность - внутренняя физическая причи­на, связанная с экспоненциальным характером изменения выход­ной величины при скачкообразном изменении входной величины (рис, 3.2)

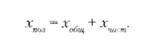Найдем полное решение X _пол дифференциального уравнения первого порядка, складывающееся из общего х_общ и частного х_част решений:

Общее решение х_общ определяет свободное движение системы при отсутсвии внешних воздействий только за счет внутреннего по­тенциала накопленной энергии.

Найдем х_о6щ из 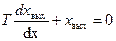в виде: х_общ = Се^р'.

Получим после подстановки ТСре^р' +Се^р' =0 характеристи­ческое уравнение Тр + 1 = 0. из которого получаем: р = -1/Т.

Частное - решение, соответствует определенному виду входной функции. Если это скачок 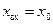, то х_част.=kx₀ и x_пол=Сe_pt+Kx₀

Найдем постоянную времени С для момента времени t = 0:

x_пол= 0, с=-kx₀

В окончательном виде полное решение запишется как:

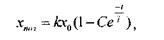
а его изображение дано на рис 3.2 а.

Коэффициент Т - постоянная времени, представляет собой отрезок прямой kx, отсекаемый касательной к экспоненте и косвен­но характеризующий время переходного процесса с точностью до 5% (t_nn =3T); k - статический коэффициент усиления, показывает степень усиления сигнала в установившемся режиме, т.е. по оконча­нии переходного процесса.

Переходным процессом называется реакция звена на скачко­образное воздействие (рис 3.3). В качестве входного воздействия могут быть приняты и другие типы возмущений (рис 3.4, 3.5).

Однако, нет необходимости исследовать реакцию элемента на всю гамму входных воздействий. В каждой из этих реакций проявятся, но по-разному одни и те же динамические свойства,

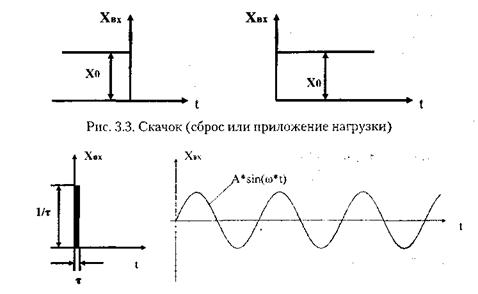
Рис. 3.4. Импульс Рис. 3.5. Периодическое

(мгновенное приложение синусоидальное воздействие

и сброс нагрузки)

т.е. в характере реакции будут проявляться одни и те же первооснов-ные свойства элемента, связанные с характером его движения.

Для данного элемента параметром интегрально оценивающим его свойства является инерционность, т.е. невозможность мгновен­но воспроизведения входной величины.

1.3.4 Колебательное звено

Это звено описывается дифференциальным уравнением вто­рого порядка:

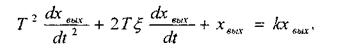
характеристическим уравнением и ПФ в виде:

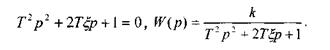
Корни характеристического уравнения комплексно-со­пряжённые при 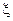<1, а переходный процесс носит колебательный характер.

Корни действительные при 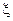>1, а переходный процесс носит апериодический характер.

Рассмотрим в качестве примера RLC-цепочку (рис.3.6). Ис­пользуя уравнения Кирхгоффа получим:

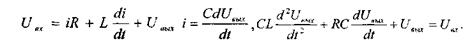
Решение уравнения второго порядка носит характер затухаю­щей синусоиды (рис.3.7).

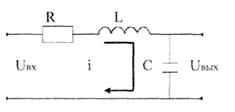Колебательный характер процесса связан с возможностью об­мена энергией между элементами звена. Для RLC - цепочки это об­мен энергией между емкостью и индуктивностью.

Коэффициент демпфирова­ния - 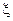определяет степень рас­сеивания энергии во внешнюю среду и степень колебательности

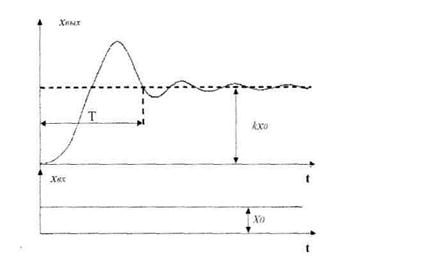Рис. 3.7. Переходная характеристика колебательного звена

переходного процесса. Чем меньше 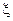тем колебатсльней переход­ный процесс.

Математически колебательный характер кривой (рис.3.6) оп­ределяется комплексными значениями корней характеристическо­го уравнения:

Т²р²+2Т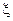р + 1 = 0.

Коэффициент Т влияет на длительность затухания функции, а коэффициент k - на ее установившееся амплитудное значение. С точки зрения физической оценки этих параметров можно сказать, что величина Т связана с временем затухания процесса, 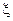- со степенью колебательности, k- со статическим коэффициентом усиления.

При 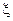= 0 рассеивания энергии нет, происходит только обмен энергией между элементами (незатухающий процесс).

1.3.5 Идеальное интегрирующее звено

Это звено описывается уравнением вида:

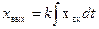с ПФ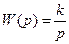

Физическим аналогом звена может служить безынерционный двигатель (рис. 3.8), для которого

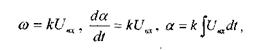
а переходная характеристика звена представляет собой прямую ли­нию с наклоном tg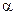= k (рис. 3.9).

1.3.6 Идеальное дифференцирующее звено

На выходе звена воспроизводится не входная величина, а ско­рость её изменения:

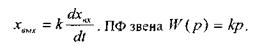
Математическая модель тахогенератора (рис. 3.10) представ­ляет собой идеальное дифференцирующее звено:

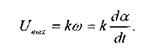
Звено реагирует на изменение входа (скачок) в виде импульса (рис. 3.11).

1.3.7 Звено с постоянным запаздыванием Моделью звена служит выражение х_еых (t) = х_а (t - т) и ПФ W(p) = е~^т. где выходная величина воспроизводится на х секунд поз­же входной. Такой моделью описывается весовой транспортер (рис. 3.12), для которого Q_BWS:(t) ⁼ Q_Hr(t' ^х)> ^а переходная характеристика (рис. 3.13) повторяет входной скачок, сдвинутый относительно на­чала координат на время т.

1.3.8 Идеальное или пропорциональное звено Звено описывается уравнениями х (t) = кх с ПФ W(j>) =» k и воспроизводит входную величину в определенном масштабе за счет статического коэффициента усиления k. Примером таких звеньев могут служить электронный усилитель (рис. 3.14) и редукторная пе­редача (рис. 3.15).

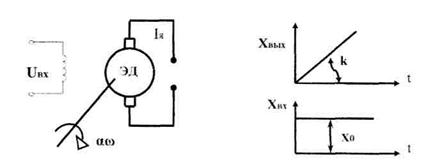
Рис. 3.8. Безынерционный ^Рис- ³⁹- Переходная

электродвигатель характеристика электродвигателя

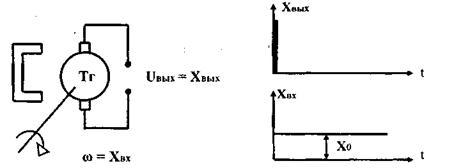
Рис. 3.10. Тахогенератор Рис. 3.11. Переходная характеристика дифференцирующего звена

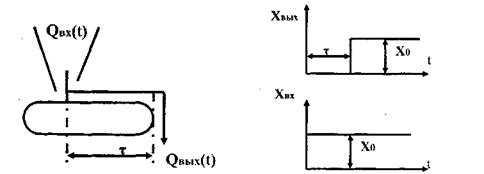
Рис. 3.12. Звено с постоянным Рис. 3.13. Переходная характеристика

запаздыванием звена с постоянным запаздыванием

Рис. 3.14. Электронный усилитель Рис. 3.15. Редукторная передача

В моделях элементарных динамических звеньев и в более сложных моделях элементов СЛУ правая часть уравнений харак­теризует способ приложения входного воздействий, а левая часть - указывает на то, как будет воспроизводиться входная величина. На­пример, в инерционном и колебательном звеньях входная величина как бы непосредственно приложена к элементу через статический коэффициент усиления k. Напротив, в дифференцирующем звене приложена как бы не сама входная величина, а ее производная, а в интегрирующем - ее интеграл. Могут быть и комбинированные спо­собы приложения входных воздействий:

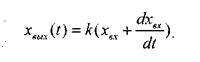
1.4 ЧАСТОТНЫЙ МЕТОД ИССЛЕДОВАНИЯ САУ

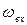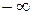1.4.1 Особенности частотного метода исследования Метод используется для анализа динамических свойств эле­ментов САУ, но при подаче на вход периодического синусоидально­го сигнала. Суждения о свойствах элемента производится по изме­нению амплитуды выходного сигнала и сдвигу фазы при изменении.от до +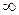Линейные модели обладают следующим свойством: при подаче на вход элемента синусоидального сигнала A sin cot вы­ходная функция А_вх sin (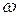t +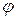) меняется в установившемся режи­ме с той же частотой, но с другой амплитудой и сдвигом фазы.

Рассмотрим апериодическое звено первого порядка. Подадим на вход звена синусоиду, на выходе получим синусоиду той же час­тоты, но другой амплитуды и сдвинутую по фазе 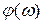относительно входного сигнала:

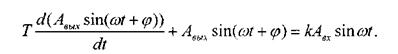
Та же картина будет наблюдаться при косинусоидальном входном сигнале:

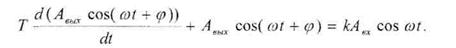
Умножая первое уравнение на j и складывая его со вторым, с учетом

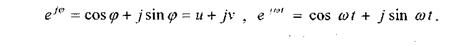
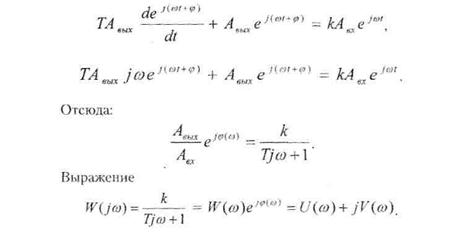
получим:

называется комплексной передаточной функцией, полученной за­меной; p =j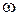в ПФ звена.

В левой части этого равенства находятся параметры, связан­ные с результатом физического проведения частотного эксперимен­та {А_вых,). В правой части этим параметрам поставлена в соответс­твие комплексная передаточная функция, что позволяет найти связь между физическими параметрами эксперимента, меняющимися с изменением со и типом и значениями коэффициентов исходной ма­тематической модели:

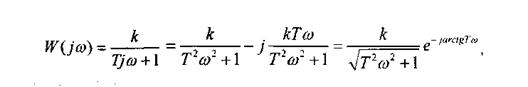
где 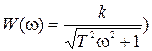- модуль комплексной ПФ.

Тогда:

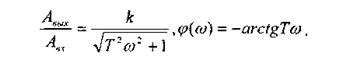
Полученные соотношения позволяют построить частотные характеристики: W(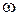) - амплитудно-частотную (АЧХ). 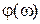- фа-зочастотную (ФЧХ) и амплитудно-фазо-частотную W(j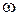) (АФЧХ) (рис. 4.1).

Частотные характеристики могут быть перестроены в лога­рифмическом масштабе с тем, чтобы добиться их более простого изображения на плоскости.

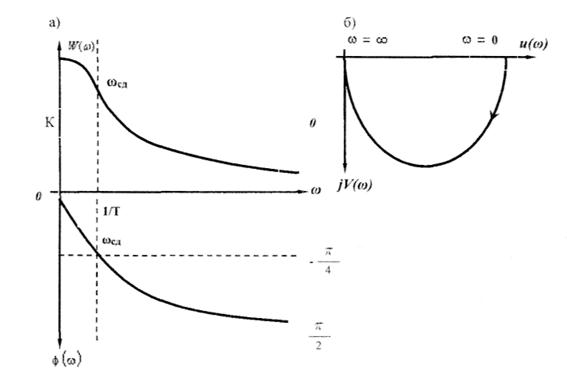
Рис. 4.1. Частотные характеристики апериодического звена а-АЧХ; б-АФЧХ

Для этого по оси абсцисс откладывается со в логарифмическом масштабе lg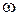, а по оси ординат - величина, L(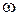)= 20 lg W(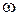). Фазо­вая частотная характеристика меняет свой масштаб только по оси абсцисс. Перестроенные таким образом частотные характеристики (АЧХ) будут называться соответственно: L(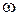) - логарифмической амплитудно-частотной характеристикой (ЛАЧХ), 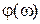- логариф­мической фазо-частотной характеристикой (ЛФЧХ).

Определим вид ЛАЧХ. Так как

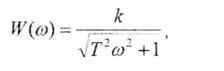
то L(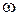) = 20lg W(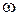) = 20lg k - 20lg.

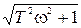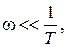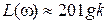В диапазоне малых частот, когдато , а в

диапазоне больших частот, когда 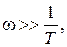то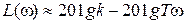

Исходная функция 20 lg 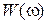аппроксимируется отрезками двух прямых (рис. 4.2).

Определим наклон второго отрезка, для чего изменим со в 10 раз. Тогда.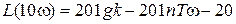

Изменение амплитуды этой прямой произошло на величину -201g 10, т.е. на -20Д6 при изменении 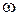на декаду, т.е. в 10 раз.

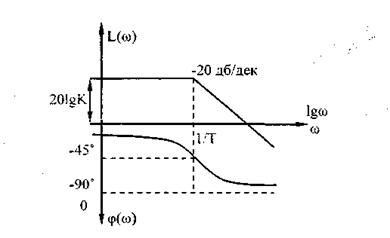
Рис. 4.2. ЛЧХ апериодического звена

ЛФЧХ имеет стандартный вид (рис. 4.2) и меняет только своё положение вдоль оси абсцисс в зависимости от значения Т.

1.4.2 Частотные характеристики колебательного звена Частотные характеристики колебательного звена строятся из следующих выражений.

Комплексный коэффициент усиления:

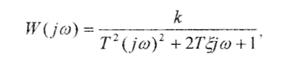
имеет модуль

и фазу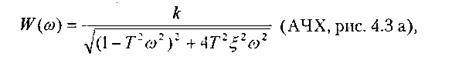

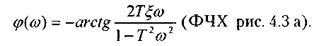
АФЧХ звена изображена на рис. 4.3 б.

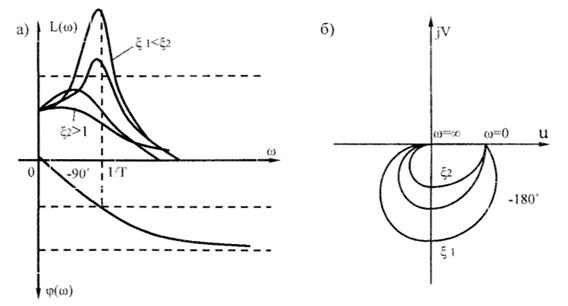
Рис. 4.3. Частотные характеристики АЧХ и ФЧХ колебательного звена: а - АЧХ и ФЧХ; б – АФЧХ

Для построения ЛАЧХ найдем:

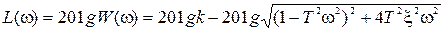
Определим ЛАЧХ в областях низких и высоких частот.

Если 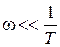, то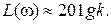

Если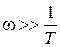, то .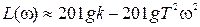

Изменим со на декаду. Тогда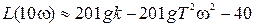. Наклон ЛАХЧ в области высоких частот составляет -40 дБ/дек.

Логарифмические частотные характеристики звена изобра­жены на рис. 4.4.

1.4.3 Идеальное интегрирующее звено Математическая модель и соответствующая ПФ звена име­ют вид:

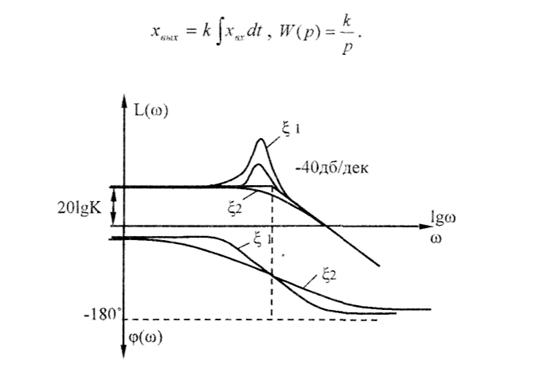
Рис. 4.4. ЛЧХ колебательного звена

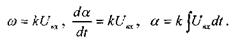
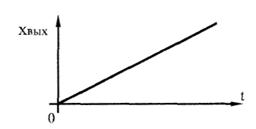Физическим аналогом зве­на может служить безынерцион­ный двигатель, для которого

Переходная характеристика звена представляет собой прямую с наклоном tg a = k (рис. 4.5).

1.4.4 Идеальное дифференцирующее звено

На выходе звена воспроизводится не входная величина, а ско­рость её изменения

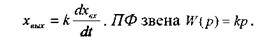
Математическая модель тахогенератора (рис. 4.6) представля­ет собой идеальное дифференцирующее звено

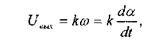
а переходная характеристика звена - импульс (рис. 4.7).

Найдем частотные характеристики идеального дифференци­рующего звена используя соотношения:

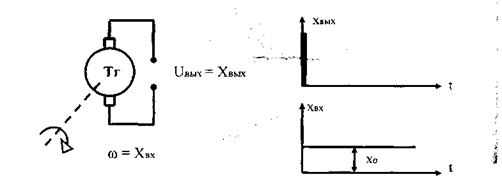
Рис. 4.6. Тахогенератор Рис. 4.7. Переходная характеристика

дифференцирующего звена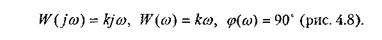

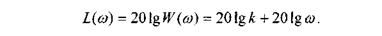
Перестроим АЧХ звена в логарифмическом масштабе:

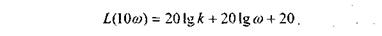
Изменение 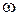на декаду дает:

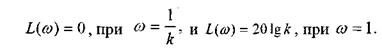
Это прямая с наклоном 20дБ/дек (рис. 4.9), принимающая значения:

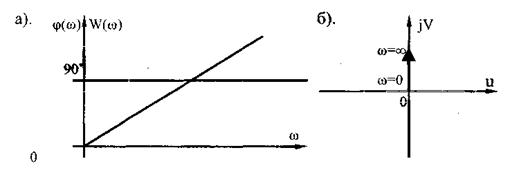
Рис. 4.8. Частотные характеристики дифференцирующего звена: а - АЧХ и ФЧХ; б -АФЧХ

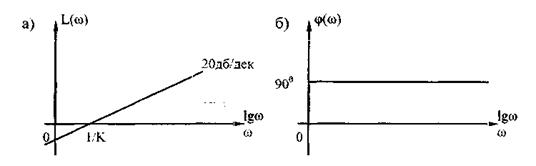
Рис. 4.9. ЛЧХ идеального дифференцирующего звена: а - ЛАЧХ; б - Л ФЧХ

1.4.5 Идеальное интегрирующее звено Для идеального интегрирующего звена замена в ПФ р на jco дает:

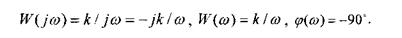
Соответствующие этим выражениям частотные характеристи­ки изображены на рис. 4.10.

ЛАЧХ звена строится из выражения

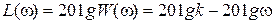
представляя собой прямую с наклоном -20 дБ/дек (рис. 4.11).

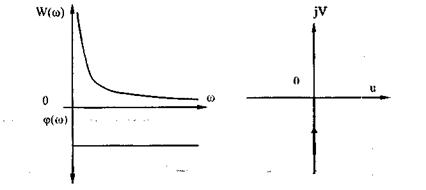
Рис. 4.10. Частотные характеристики интегрирующего звена:

а - АЧХ и ФЧХ; б - АФЧХ

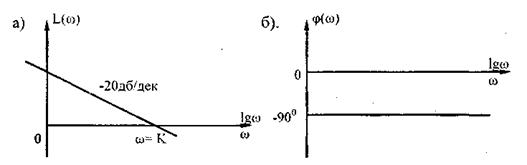
Рис. 4.11. ЛЧХ идеального интегрирующего звена: а - ЛАЧХ; б - ЛФЧХ

1.4.6 Звено с постоянным запаздыванием Для звена с постоянным запаздыванием частотные характе­ристики (рис. 4.13) получаются из выражений:

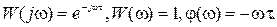
Логарифмические частотные характеристики звена изображе­ны на рис. 4.14.

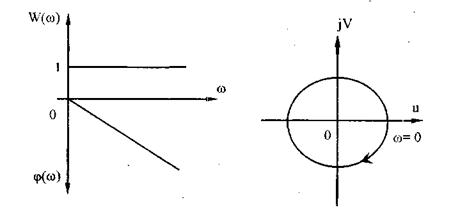
Рис. 4.13. Частотные характеристики звена с постоянным запаздыванием: а - АЧХ и ФЧХ; б - АФЧХ

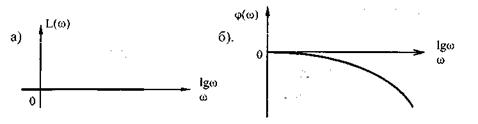
Рис. 4.14. ЛЧХ звена с постоянным запаздыванием: а-ЛАЧХ;б-ЛФЧХ