Оценки числовых характеристик по выборке

Выборка и ее характеристики

Рассчитать значения числовых характеристик генеральной совокупности (в частности математического ожидания и дисперсии) по формулам (3.14) - (3.17) можно только в том случае, если вся генеральная совокупность находится в распоряжении исследователя. Это очень редкий, крайний случай, при котором случайная величина фактически превращается в детерминированную. На практике исследователь имеет дело с конечным набором реализаций случайной величины, полученным в результате эксперимента. Такой набор называется выборкой

(х₁, х₂, х₃,..., х_N-1, x_N )

Число полученных экспериментальных результатов N называется объемом выборки.

Основная задача математической статистики заключается в том, чтобы по результатам эксперимента (по данным выборки) сделать обоснованные выводы о свойствах генеральной совокупности.

Выборка должна достаточно полно характеризовать генеральную совокупность, иными словами, она должна быть представительной. Чтобы представительность была обеспечена, необходимо выполнение двух важных условий: во-первых, все элементы генеральной совокупности должны иметь возможность появляться в выборке с одинаковой вероятностью; во-вторых, наблюдения должны быть независимыми, то есть появление каждого из элементов выборки не должно влиять на вероятность появления других элементов. Приведенные выше условия сформулированы для дискретной случайной величины. Аналогичные условия нетрудно сформулировать и для непрерывной генеральной совокупности.

Так как элементы выборки случайны, все заключения и результаты, полученные на основе выборочных данных, носят вероятностный характер.

Выборка содержит лишь часть генеральной совокупности, по которой можно попытаться оценить числовые характеристики всей генеральной совокупности. Для этого предложены различные формулы. Следовательно возможны различные оценки одной и той же числовой характеристики (например, математического ожидания) по результатам одной и той же выборки. Конечно, хотелось бы, чтобы оценки были “хорошими”, близкими к той величине, которую они оценивают. Но что это означает? Существуют три меры близости к оцениваемому параметру:

- несмещенность - равенство математического ожидания оценки значению соответствующей числовой характеристики при любом объеме выборки;

- состоятельность - сходимость по вероятности оценки к оцениваемому параметру (выражается в том, что при увеличении объема выборки оценка приближается к оцениваемому параметру числовой характеристики);

- эффективность - мера рассеяния оценки в окрестности оцениваемого параметра. Эффективная оценка обладает наименьшей дисперсией по сравнению с другими оценками данной числовой характеристики.

Чаще всего в качестве оценки математического ожидания используется среднеарифметическое значение :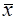

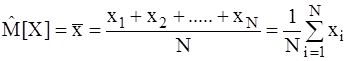. (3.20)

Здесь 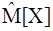обозначает оценку М[X]. Эта оценка является несмещенной, состоятельной, а для нормального распределения - эффективной.

Другой возможной оценкой математического ожидания является полусумма максимального и минимального значения случайной величины, полученных в выборке:

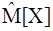
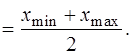(3.21)

Эта оценка несмещена, состоятельна для симметричных распределений, но эффективна только для равномерного распределения.

Для нахождения оценок дисперсии 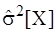чаще всего используются следующие формулы:

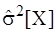
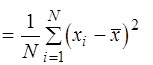(3.22)

и

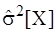
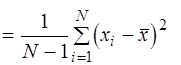. (3.23)

Оценка (3.22) состоятельна, эффективна для нормального распределения, но смещена. Она, следовательно, вносит некоторую систематическую погрешность.

Оценка (3.23) лишена этого недостатка. Она несмещена, состоятельна, но для нормального распределения неэффективна. Обычно предпочитают пользоваться несмещенной оценкой (3.23).

Приведенные выше оценки числовых характеристик генеральной совокупности называются точечными оценками. Получение точечных оценок дает важную информацию, но не позволяет судить о степени их близости к оцениваемой числовой характеристике. Более содержательны процедуры оценивания, связанные с определением интервала, который накрывает оцениваемое значение с известной степенью достоверности. Такие процедуры являются интервальными оценками.

Возможно, у читателя возникнет вопрос, какое отношение приведенные сведения о генеральной совокупности, выборке, оценках числовых характеристик имеют к науке об измерениях. Имеют и самое непосредственное. Дело в том, что при проведении измерительного эксперимента постулируется, что истинное значение измеряемой величины совпадает с математическим ожиданием результатов наблюдений, неопределенность полученного результата измерений характеризуется средним квадратическим значением погрешности, которое равно корню квадратному из дисперсии, а возможные значения результатов наблюдений представляют собой генеральную совокупность, обладающую некоторым законом распределения. Получение результатов параллельных наблюдений, то есть независимых наблюдений, проведенных при одинаковых условиях, отождествляется с извлечением выборки. Таким образом, решая задачу оценивания, мы одновременно решаем измерительную задачу.