Задачи оптимальной правильной раскраски графов

Пусть задан неориентированный граф без петель G (X, V) порядка n, X ={ x ₁,… …, x_n } – множество вершин; V Í X ´ X – множество ребер.

Под раскраской вершин графа понимается процедура приписывания цветов (меток) вершинам графа G (X, V). Правильной раскраской графа в k цветов (k -раскраской графа) считается такая раскраска вершин графа G (X, V), при которой никакие две смежные вершины x_i, x_j Î X, x_i ¹ x_j не получают одинакового цвета.

Наименьшее число k, такое, что граф G (X, V) является k -раскрашиваемым, называется хроматическим числом графа G (X, V).

Задача нахождения хромати­ческого числа графа называется задачей о раскраске (правильной раскраске) графа. Соответствующая этому числу раскраска вершин разбивает множество вершин на k подмножеств, каждое из которых содержит вершины одного цвета. Эти множества вершин одного цвета называется одно­цветным классом и являются независимыми, так как в пределах одного множества нет двух смежных вершин.

На практике чаще приходится с несколько иной задачей, связанной с пра­виль­ной вершинной раскраской – задачей выделения максимального k - хрома­ти­ческого подграфа. Данная задача формулируется следующим образом.

Пусть задан неориентированный взвешенный граф G (X, V, d) порядка n, где X ={ x ₁,…, x_n } – множество вершин; V Í X ´ X – множество ребер; d: X ® R ⁺– отображе­ние, определяющее вес каждой вершины, где R ⁺ – множество действительных неотри­ца­тельных чисел. Требуется для заданного числа цветов k выделить в исходном графе G (X, V, d) k -хро­мати­ческий подграф с максимальным весом:

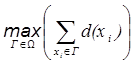
(4)

где W ­­– множество всевозможных k -раскрашиваемых подграфов исходного графа G (X, V, d).

В качестве варьируемых параметров здесь выступают: во-первых, распре­деление множества вершин исходного графа на k +1 подмножества (k -одноветных класса раскрашиваемого подграфа и одно не раскрашиваемое); во-вторых, размер­ности цветовых классов. Таким образом можно трактовать поставлен­ную задачу как однокритериальную с двумя степе­нями свободы.

Еще ряд задач из рассматриваемого класса, выбранные в качестве тестовых графовых проблем, заключаются в равномерном разбиении множества вершин графа. Под равномерностью здесь понимается приблизительно равное соотноше­ние весов (суммарный вес вершин из одного класса) одноцветных классов. Задачи такого рода уже имеют три типа варьи­ру­емых параметров. Во-первых, распре­деление множества вершин исходного графа на k одноцветных классов. Во-вторых, размер­ности цветовых классов. В качестве третьего варьи­ру­емого параметра выс­ту­пает k – число цветов.

Потребуем, чтобы исходный граф G (X, V, d) был полностью правильно раскрашен. Данное условие определяет область поиска D – мно­жество всевоз­можных правильных раскрасок исходного графа. Так, если в качестве критерия оптимальности исполь­зовать минимизацию числа используемых цветов в правиль­ных раскрасках, то получим классическую задачу раскраски графа.

Обозначим через X ₁,…, X_k – множества одноцветных классов k -хрома­тического гра­фа; s_i – суммарный вес вершин множества X_i (т.е. суммарный вес независимых вершин):

;

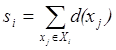(5)

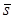– средний вес одноцветных классов:

.

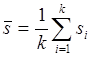(6)

Потребуем, чтобы суммарный вес вершин для всех одноцветных классов отличался от среднего как можно меньше. То есть необходимо осуществить пра­виль­ную раскраску вершин графа G (X, V, d) таким образом, чтобы минимизировать целевую функцию:

.

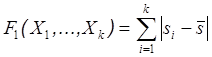(7)

Тогда оптимальным решением будет правильная раскраска (X ₁^*,…, X_k ^*)Î D графа G (X, V, d) такая, что

.

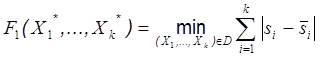(8)

Также для выравнивания весов одноцветных классов можно максимизи­ровать вес минимального из получившихся одноцветных классов:

.

(9)

В этом случае оптимальной будет правильная раскраска (X ₁^*,…, X_k ^*)Î D графа G (X, V, d) такая, что

.

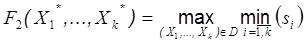(10)