Некоторые свойства и особенности применения энергетических спектров и корреляционных функций

 

Рассмотрим некоторые свойства и особенности применения энергетических спектров и корреляционных функции аномалий, которые будут широко использованы в последующих разделах.

1. Теорема Парсеваля

Пусть функция f(х) имеет спектр S(ω). Интегрируя по ω в бесконечных пределах обе части равенства (1.4), найдем

 

 

На основании равенства (1.3) получим

 

 

С учетом формулы (1.1) окончательно найдем

 

 

где учтено, что функция |S(ω)| — четная. Эту формулу обычно называют теоремой Парсеваля или теоремой Релея.

Аналогично для трехмерных аномалий на основании равенств (1.16), (1.12) и (1.10) для теоремы Парсеваля получим

 

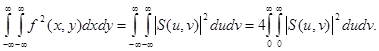
Для трехмерных аномалий, симметричных относительно вертикальной оси, переходя к полярным координатам, отсюда найдем

 

 

Эту формулу можно получить и из равенства (1.21) (умножая обе его части на ρ и интегрируя по ρ в пределах от 0 до ∞) с учетом выражений (1.10) и (1.20).

Теорема Парсеваля, учитывающая величину полной энергии аномалий, имеет важное значение в гравиразведке и магниторазведке. Она использовалась в работах многих исследователей (К.В. Гладкий и др.). С ее применением В.Н. Страховым были получены ряд фундаментальных формул спектрального анализа гравитационных и магнитных аномалий.

2. Выражение энергетических спектров и корреляционных функций одних аномалий через другие

Пусть f_x(x, y), f_y(x, y), f_z(x, y) — производные по осям координат x, y и z от некоторой гравитационной или магнитной аномалии f(х, y) (от гравитационного или магнитного потенциала, от ускорения силы тяжести и т.д.). Тогда пользуясь теоремами о спектрах производной функции, после небольших преобразований получим:

 

 (1.22)

 

Практически наиболее важными являются случаи f = U и f = V_z, где U — магнитный потенциал, V_z — ускорение свободного падения. Для этих случаев последнее равенство можно переписать в виде:

 (1.23)

 (1.24)

 

Из этих равенств можно определить (заменить) энергетический спектр одной из аномалий: X, Y, Z или V_xz, V_yz, V_zz через известные значения энергетических спектров других аномалий. Этот вывод можно перенести и на случай автокорреляционных функций:

 

 (1.25)

. (1.26)

 

В двухмерном случае (при ) из равенств (1.23)-(1.26) получим

 

 (1.26а)

 

Из этих равенств видно, что в двухмерной задаче энергетические спектры и автокорреляционные функции аномалий H, Z или гравитационных V_xz, V_хх, V_zz полностью взаимозаменяемы. Некоторые из них показаны на рис. 6. Это же положение верно в двухмерном случае и для аномалий V_х, V_z, т.е. для горизонтальной и вертикальной производных от любой исходной одной и той же аномалии. Оно же верно и для аномалий H, Z в случае косого и вертикального намагничивания и для нормированных функций Q и B аномалий H, Z и ΔT.

Это важное свойство автокорреляционных функций и энергетических спектров. Им не обладают исходные гравитационные и магнитные аномалии, за исключением функций V_xz, V_хх, V_zz в трехмерном случае и V_хх и V_zz — в двухмерном, для которых указанное свойство следует из уравнения Лапласа.

Легко показать, что энергетический спектр аномалии является всегда вещественной и четной функцией. Тогда и автокорреляционная функция аномалии будет вещественной и четной функцией. Рассмотрим взаимные энергетические спектры Q₁₂(ω) и Q₂₁(ω) двух функций f₁(x) и f₂(x). Для них верны соотношения

 

Рис. 1. Примеры разных аномалий, которым соответствуют одни и те же автокорреляционная функция B(τ) и энергетический спектр Q(ω)

 

, (1.27)

 (1.28)

 (1.29)

 

Кроме того, легко показать, что произведение Q₁₂Q₂₁ и сумма Q₁₂ ⁺ Q₂₁ являются всегда четными функциями, а разность Q₂₁ – Q₁₂ — всегда мнимой. При этом, если одна аномалия четная, а вторая нечетная, то

 (1.30)

 

Здесь, если первая функция — это , а вторая , где f — некоторая исходная аномалия (в двухмерном случае, например, для функций V_x, V_z; V_xz, V_zz для магнитных аномалий H и Z, если одна из них четная, а вторая - нечетная), то учитывая доказанное выше равенство Q_p = Q_q получим для суммы аномалий F = p + q:

 

 (1.31)

 

для взаимного энергетического спектра:

 

 (1.32)

 

Что же касается взаимных корреляционных функций, то для них получим

 

 

где В₁₂(τ) + В₂₁(τ) — четная функция; В₂₁(τ) – В₁₂(τ) — нечетная функция.

Кроме того, из равенств (1.30), (1.31) и (1.32) соответственно получим (если одна из аномалий четная, вторая — нечетная)

 

, (1.33)

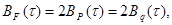 (1.34)

 (1.35)

Полученные равенства можно использовать для замены выражений Q₁₂, Q₂₁ и B₁₂ через значения Q₁, Q₂ и B₂₁ при решении различных задач, в частности, при определении радиуса корреляции суммарного поля, состоящего из нескольких компонент — региональной, локальной составляющих и ошибок наблюдений; при определении возможности наличия корреляции между двумя сигналами и т.д. Из изложенного материала видно, что корреляционные функции и энергетические спектры аномалий обладают рядом других важных свойств, которые при решении многих задач гравиразведки и магниторазведки делают их применение предпочтительнее, чем применение самих аномалий. Прежде всего это то, что корреляционные функции и энергетические спектры аномалий являются некоторыми интегральными характеристиками, т.е. при определении их значений (хотя бы одного) используются все точки исходной аномалии — вся кривая, что приводит к значительному уменьшению случайных погрешностей инструментального и геологического характера. Влиянию ошибок наблюдений подвергается только центральная часть кривых корреляционных функций, что делает возможным исправление их значений в этой центральной части.

Для случая автокорреляции ближайшая к поверхности особая точка получаемых функций залегает в 2 раза глубже. Этот факт расширяет области применения различных трансформаций к значениям автокорреляционной функции.

Автокорреляционные функции и энергетические спектры аномалий для производных одного порядка взаимозаменяемы (в двухмерном случае равны), что позволяет по данным В или Q для аномалии одной производной определить значения рассматриваемых функций для аномалий другой производной или, если известны значения аномалий двух производных, например, Z и H повышать точность вычисления функции B и Q Взаимозаменяемость находит, например, широкое применение при совместной интерпретации данных гравитационного и магнитного полей.

Функции B и Q являются всегда четными, и этот факт облегчает возможность получения различных соотношений, упрощает кривые и делает их более пригодными для определения формы, размеров и глубины залегания аномальных тел.

В то же время следует отметить, что из-за четности автокорреляционных функций и энергетических спектров аномалий в них пропадают полезные эффекты, связанные с асимметричностью кривых аномалий и косым намагничиванием магнитных масс. Это вызвано тем, что указанные функции формируются только значениями амплитудного спектра, влияние же фазового спектра в них отсутствует. Как раз этим и объясняется то, что аномалии с равными амплитудными и разными фазовыми спектрами имеют одни и те же энергетические характеристики — функции B и Q. Поэтому полезное свойство

четности их кривых в некоторых случаях является их недостатком. Но применение энергетических характеристик аномалий основано на использовании их полезных свойств. Полезные же эффекты асимметричности косого намагничивания аномалий четко отражаются на значениях взаимных энергетических спектров и взаимных корреляционных функций, и при необходимости их можно определить из значений этих функций.