Или все формулы системы функциональных уравнений имеют решения, или же в системе уравнений нет ни одной такой формулы

Для обоснования данного, довольно – таки экзотического на сегодняшний день метода, далее будут рассмотрены некоторые известные задачи. 

                          

Уравнение Пелля.

                      (1)

 

Рассмотрим 3 варианта:

- IХ - чётное число, У - нечётное число, n - нечётное число;

- II Х - нечётное число, У - нечётное число, n - чётное число;

- III Х - нечётное число, У - чётное число, n – любое, и чётное, и нечётное число.

И всегда ½ Х ½ > ½ У ½

 

Вариант I.  

Составим функциональное уравнение.

 

, где, конечно же, ₁ > ₂

Возьмём к = - ₂, тогда

 

После преобразований

                                                           (2)

где ; .

Окончательно, после подстановки будет

, где n = 3, 15.....

Проверим при n = 3

а) , 

б) , 

Подставим (а) в уравнение (1)

     

                                

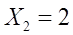
Для случая Х = 2, У = 1, n = 3 будет

Подставим (б) в уравнение (1)

      

Для        

Проверка даёт

Для            

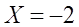
Проверка даёт

Составим последующее функциональное уравнение.

 

После упрощения

где ,

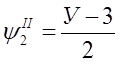
После подстановки

Следующее функциональное уравнение примет вид

 

После упрощения

где ,

 

 

После подстановки

 

Получилась система бесконечных решений:

 

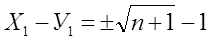
                                                  (3)

    …………………………..

 

   

Вариант II.

Функциональное уравнение примет вид.

 

После преобразований будет

 

, где n чётные числа n = 8, 24 ……

 

Само же выражение идентично формуле (2).

Система бесконечных решений примет вид системы (3).

Тогда система решений (3) будет общей для вариантов I и II при n – чётных и нечётных числах.

 

Вариант III.  

Также напишем функциональное уравнение.

 

 

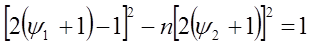
Опускаю все вычисления, - напишу окончательный результат:

 

    …………………………..

 

   

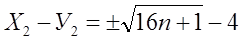
На решении данного уравнения Пелля подтверждено следующее утверждение из доказательства ВТФ:

 

Или все формулы системы функциональных уравнений имеют решения, или же в системе уравнений нет ни одной такой формулы.

 

Мне не приходилось встречать классического решения этого уравнения, - для меня это чистый экспромт. Специалисты могут сравнить.

    Вообще же, этим методом решается любое уравнение вида:

                     ,

а уравнение Пелля лишь как частный случай, при t = 2 и N = 1.

Уравнение  

    .                  (1)

(У²=Х³-Х, У²=Х³-Х+1, У²=Х³+аХ+В)

Рассмотрим 4 варианта:

- IУ - нечётное число, Х - нечётное число, К - чётное число;

- II У - нечётное число, Х - чётное число, К - нечётное число;

- III У - чётное число, Х - чётное число, К - чётное число;

- IV У - чётное число, Х - нечётное число, К - нечётное число.

Решение этого уравнения принципиально ни чем не отличается от решения уравнения Пелля, - в обоих уравнениях наличие двух переменных.

Вариант I.

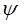Во всех четырёх вариантах У > Х, и следовательно ₁> ₂

     

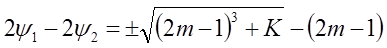
Тогда будет

                                      (2)

Получилась система уравнений (1) и (2).