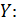2020-05-12
124
Пусть случайная величина 
– доходность некоторого актива (например, акции), известно ее распределение, то есть значения доходности 
и их вероятности 
за рассматриваемый промежуток времени. Тогда математическое ожидание 
выражает среднюю (прогнозную) доходность актива.
Свойства.
Свойство 1. Математическое ожидание постоянной величины равно ей самой.
.
Доказательство.
|
|
| 
|
|
|
| 
|
.
Свойство 2. Постоянный множитель можно вынести за знак математического ожидания.
Доказательство.
|
|
| 
| 
| … | 
| … |
|
| 
| 
| … | 
| … |
|
| 
| 
| … | 
| … |
|
|
| … |
| … |
Свойство 3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.
Доказательство.
Для простоты будем считать, что и 
принимают конечное число значений.
Обозначим 
, 
, 
.
Замечание.
Формула обобщается на любое число слагаемых
.
Свойство 4. Если случайные величины и независимы, то математическое ожидание их произведения равно произведению математических ожиданий:
.
Доказательство.
Опять рассмотрим для простоты конечное число возможных значений.
|
|
|
|
| … |
|
| 
| 
| 
| … | 
|
|
|
|
| … |
|
| 
| 
| … | 
|
|
(
вынесем за знак )
Свойство 5. Если 
– числовая функция и – дискретная случайная величина, то
Свойство 6. Если – выпуклая функция, то
– неравенство Йенсена.
(Выпуклость функции – это выпуклость вниз
, где 
.
Дисперсия
Рассмотрим пример:
|
|
| -100 | -50 | 50 | 100 |
|
| -0,02 | -0,01 | 0,01 | 0,02 |
|
| 
|
|
|
|
|
|
|
|
|
.
Математическое ожидание не полностью характеризует случайную величину; нужно выяснить, насколько рассеяны ее возможные значения вокруг центра, то есть математического ожидания. Для этого вводят новую числовую характеристику, называемую дисперсией. Слово «дисперсия» означает «рассеяние».
Назовем случайную величину – 
, где 
отклонением.
|
| 
| 
| … | 
| … |
|
|
| … |
| … |
На первый взгляд, кажется, что нужно найти среднее значение (математическое ожидание) отклонения случайной величины от ее центра, но
.
Поэтому вычисляют среднее значение квадрата отклонения. Это и есть дисперсия.
(Величина 
- среднее значение модуля отклонения, называемая средним линейным отклонением неудобна в пользовании).
Определение.
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
Для дискретной случайной величины
| (если число возможных значений конечно) |
|
| (если число возможных значений бесконечно) |
|
и
неслучайная постоянная величина, она имеет размерность квадрата случайной величины, что не всегда удобно, Поэтому в качестве меры рассеяния (разброса) возможных значений случайной величины вокруг ее математического ожидания используют величину 
, имеющую ту же размерность и называемую средним квадратичным (квадратическим) отклонением случайной величины или стандартным отклонением.
Если дисперсия характеризует средний размер квадрата отклонения, то 
можно рассматривать как некоторую среднюю характеристику самого отклонения, точнее, величины 
.
.
В финансовом анализе.
Если случайная величина – доходность некоторого актива, то дисперсия 
или – выражает меру отклонения доходности от ожидаемого среднего значения, то есть риск данного актива.
ТЕОРЕМА.
Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.
. (*)
Доказательство.
Следствие.
.
Свойства.
Свойство 1. Дисперсия постоянной величины равна нулю.
(постоянная величина не имеет рассеяния).
Доказательство.
.
Свойство 2. Постоянный множитель выносится за знак дисперсии в квадрате 
.
Доказательство.
.
Свойство 3. Рассмотрим дисперсию суммы
.
Величина 
называют ковариацией или корреляционным моментом случайных величин и , и обозначают 
или σ(X,Y).
.
Ковариация имеет размерность произведения размерностей случайных величин и .
ТЕОРЕМА.
Если и независимы, то их ковариация равна нулю.
