Необходимое условие экстремума функционала

Различают сильный и слабый локальный минимум (максимум) функционала.

Говорят, что функционал  достигает на кривой  сильного минимума (максимума), если  в сильной e - окрестности кривой .

Говорят, что функционал  достигает на кривой  слабого минимума (максимума), если  в слабой e - окрестности кривой .

Замечание. Всякий сильный экстремум функционала является и слабым. Обратное, вообще говоря, неверно.

Необходимое условие экстремума функционала.

Если функционал , имеющий вариацию, достигает минимума или максимума на кривой , где  есть внутренняя точка области определения функционала, то при  первая вариация функционала равна нулю: .

Замечание. Различие между сильным и слабым экстремумом не имеет существенного значения при выводе достаточного условия экстремума, но весьма существенно при выводе и применении достаточных условий экстремума.

При выводе достаточных условий экстремума функционала для различных постановок вариационных задач применяется следующая важная лемма.

Основная лемма вариационного исчисления.

Если для каждой непрерывной функции  

,                                                                 (21)

где функция  непрерывна на отрезке , то на том же отрезке.

Замечание. Утверждение основной леммы вариационного исчисления не изменится, если на функцию  наложить следующие дополнительные ограничения:  имеет непрерывную на отрезке  производную и

Рассмотрим необходимое условие экстремума для интегрального функционала вида

,                                                (22)

где функция  непрерывна вместе со своими первыми частными производными .

Первая вариация функционала, вычисленная по второму способу (см. п. 2.3), будет определяться формулой:

 .                                    (23)

Для вычисления частной производной под знаком интеграла введем переменные . Тогда

.                               (24)

Учитывая, что при , из (23) с учетом (24) получаем

                                                 (25)

    Таким образом, необходимое условие экстремума функционала (22) имеет вид

.                                       (26)

Задачи с фиксированными границами.

Уравнение Эйлера

Рассмотрим множество М допустимых функций, удовлетворяющих следующим условиям:

- функции  определены и непрерывно дифференцируемы на интервале где  и заданы, т.е.  

- функции  удовлетворяют граничным условиям

                                                        (27)

где значения  и заданы, т.е. кривые проходят через две закрепленные граничные точки.

На множестве М задан функционал

                                                       (28)

где подынтегральная функция  имеет непрерывные частные производные до второго порядка включительно по всем переменным.

Среди допустимых функций (кривых)  требуется найти функцию (кривую) , на которой функционал (28) достигает экстремума, т.е.

                                                 (29)

и на кривые не наложены никакие дополнительные условия, кроме граничных условий (27).

Поскольку в граничных точках функции x(t) принимают фиксированные значения, вариации функций в граничных точках равны нулю:

                                              (30)

Первая вариация функционала (28) определяется полученной ранее формулой (25), которую можно разложить на сумму двух интегралов:

.                                (31)

Проинтегрируем второй интеграл в формуле (31), используя правило интегрирования по частям .

Обозначим , тогда

.       (32)

Подставляя полученный результат в (31) с учетом (30) получаем

                                                     (33)

Необходимое условие экстремума функционала , откуда

.                                                         (34)

В уравнении (34) вариация   - произвольная непрерывная на  функция, поэтому согласно основной лемме вариационного исчисления из (34) следует

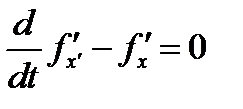                                                                (35)

Уравнение (35) называется уравнением Эйлера для функционала и является необходимым условием экстремума функционала (28) с граничными условиями (27). Функции , удовлетворяющие уравнению (35), называются экстремалями функционала.