2020-06-29
97
а) Площадь плоской фигуры 
, если 
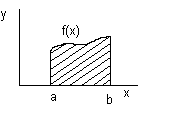
Если 
на интервале интегрирования, то рассматривают интеграл от модуля (или изменяют знак). 
или 
.
Пример 1. Найти площадь фигуры, ограниченной графиком 
и осью абсцисс, если 
.
.
Более удобной является формула: 
где 
.
y
f 2(x)
f 1(x)
0 х
Пример 2. Найти площадь, ограниченной параболой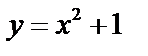 
и прямой 
.
б) Пусть функция задана в параметрической форме: 
.
.
Пример 3. Вычислить площадь одной арки циклоиды 
.
.
.
M
N
0 
x
в) Если кривая задана в полярных координатах: 
.
Разобьем данную площадь радиус – векторами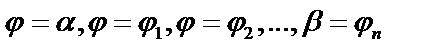 
на n частей. Пусть углы между радиус – векторами равны 
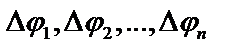Площадь 
сектора: 
.
Площадь: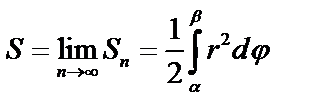 
.
Пример 4. Найти S, ограниченную кардиоидой: 
.
Вычислить половину площади:
.
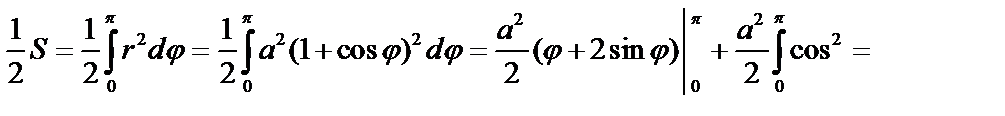
Длина дуги кривой
а) Пусть кривая задана уравнением 
. Возьмем на 
точки 
, и проведем хорды, которые обозначим 
. Получим ломанную 
, вписанную в дугу 
. Длина ломаной: 
. Длина дуги – предел: 
. Если на отрезке 
непрерывны, то этот предел существует. Пусть 
, тогда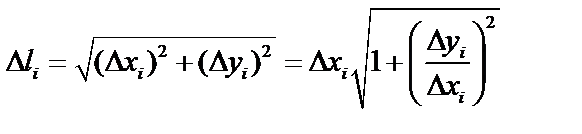 
. По теореме Лагранжа 
, 
, по условию, 
и 
– непрерывны, поэтому существует предел интегральной суммы, который равен определенному интегралу:
.
Пример. Найти длину дуги кривой 
.
.
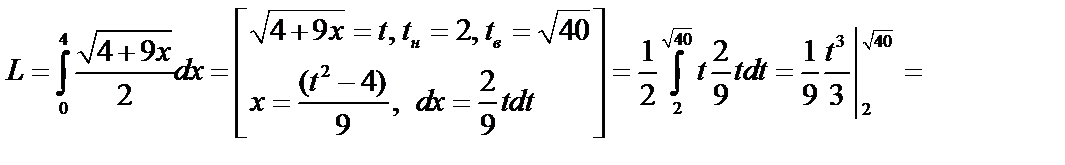
б) Если кривая задана параметрически: 
то длина дуги
.
в) Пусть кривая задана в полярных координатах: 
тогда 
.
;
;
тогда 
.
Пример. Найти длину дуги кардиоиды: 
.
; 
;
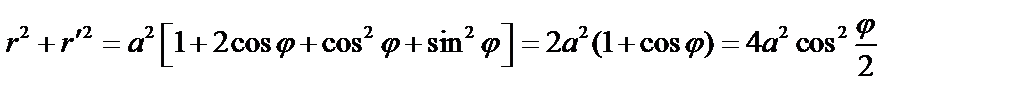длина дуги: 
.
Вычисление объема и площади поверхности вращения.
Пусть имеется тело, для которого известна площадь сечения, перпендикулярного оси ох, т.е. 
. Проведем плоскости, перпендикулярные оси ох. Они разобьют тело на слои, 
(цилиндр), тогда 
. Переходя к пределу: 
.
Объем тела вращения:
Если ось вращения – ось O Y, то объем тела вращения: 
.
Если ось вращения – ось O X, то объем тела вращения: 
и 
.
Площадь поверхности вращения.
Разобьем 
на 
частей и проведем ломаную. При вращении ломаной получаются усеченные конусы (цилиндры). Площадь поверхности 
, длина хорды 
, 
.
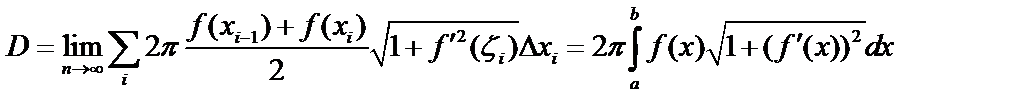Пример: Объем тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями: 
и 
.
.
.
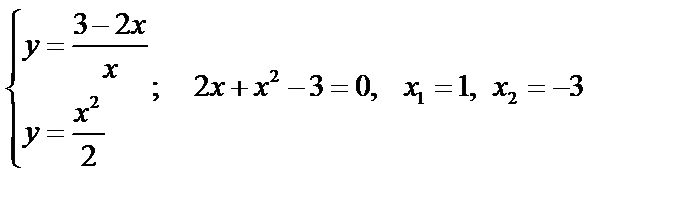Глава 12. Дифференциальные уравнения
