Площадь поверхности цилиндра

Полная поверхность цилиндра состоит из площадей двух оснований и площади боковой (цилиндрической) поверхности, т.е. S_цил = 2 S_осн + S_{бок. пов.,}  при этом

 где r – радиус цилиндра.

Чтобы найти площадь боковой поверхности, сделаем ее развертку. Для этого «разрежем» боковую поверхность цилиндра по образующей и развернем. Несложно догадаться, что получим прямоугольник.

Разверткой боковой поверхности цилиндра является прямоугольник. Одна сторона этого прямоугольника равна высоте цилиндра, а другая равна длине окружности, которая «опоясывает» основание.

Тогда:    S_{бок. пов} = 2π r ∙ h                    Имеем:

 

Решение задач

Задача 1. Площадь боковой поверхности цилиндра равна 16π, диаметр основания - 8. Найдите высоту цилиндра.

Решение. .                          Ответ: 2

Задача 2. Площадь боковой поверхности цилиндра равна 56π, высота – 7. Найдите площадь осевого сечения цилиндра.

Решение. . Значит, необходимо найти радиус основания (или диаметр).  тогда .          Ответ: 56 кв. ед.

 Задача 3. Осевое сечение цилиндра – квадрат, диагональ которого равна 20см.

 Найти: а) высоту цилиндра, б) площадь основания цилиндра.

      

                    Дано: цилиндр 

                    Осевое сечение: ABCD – квадрат, BD = 20см

                    Найти: 1) h 2) S_осн

 

     Решение:

1) h из ΔABD: AD = AB    

2) S_осн =                              Ответ: см, S_осн = 50π см²

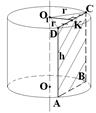
Задача 4. Высота цилиндра равна 10м. Площадь сечения цилиндра плоскостью, параллельной оси цилиндра и удаленной от нее на 9м, равна 240 м². Найти радиус цилиндра.

 

           Дано: цилиндр, h = 10м

           ABCD – сечение, S_сеч = S_ABCD = 240 м²

            d = O₁K = 9м

 

                                             Найти: r

                                  Решение:

1) r = O₁D из ΔDO₁K:

      O₁D² = DK² + O₁K², DK -?

 

  2) DK: из S_ABCD = 240

                         AD ∙ DC = 240, AD = h =10, DC = 24, DK = 12

 

                             3)                                               Ответ: 15м

Задача 5. Высота цилиндра на 12 см больше его радиуса, а площадь полной поверхности равна 288π см². Найти радиус основания и высоту цилиндра.

 

В этой задаче рисунок делать не нужно. Она алгебраическая.

Дано: цилиндр, r

            h = (r + 12) см S_цил = 288π см²                        Найти: r, h  

Решение: пусть радиус – это x (x >0, т.к. это физическая величина). Тогда h = x + 12

Подставим обозначения в формулу: S_цил =

S_цил = 2π x (x + x + 12), 288π = 2π (2x² + 12x) Сократив уравнение на 2π, имеем:

первый корень не удовлетворяет условию x >0. Тогда: r = 6, h = 18                                                                                                Ответ: r = 6см, h = 18см

 

Сфера и шар

Определения

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. Данное расстояние – это радиус сферы R, данная точка – центр сферы O.

Любой отрезок, соединяющий центр и какую-нибудь точку сферы, является ее радиусом. Отрезок, соединяющий две точки сферы и проходящий через центр – диаметр. Очевидно, что диаметр равен 2R.

Шар – это тело, ограниченное сферой. Шар изображается так же, как сфера.

Сфера как тело вращения получается вращением полуокружности вокруг диаметра. Шар – вращением полукруга.

 

Уравнение сферы

Если поместить сферу в систему координат, можно получить уравнение сферы.

По аналогии с уравнением окружности:

       Уравнение окружности:

где x₀ и y₀ – координаты центра окружности точки С: С(x₀; y₀), R – радиус окружности.

Если координаты точки М(x, y) удовлетворяют уравнению, значит, точка М  лежит на окружности. (Удовлетворяют – значит, при подстановке координат в уравнение получается верное числовое равенство.)

 

 Для сферы уравнение похожее, только мы переходим от плоскости к пространству, т.е. появится еще одна координата.

Уравнение сферы: , 

       где x₀, y₀, z₀ – координаты центра сферы: С(x₀; y₀. z₀), R – радиус сферы.

 

Например: 1) Напишите уравнение сферы радиуса R с центром в точке C, если C (2; -3; 7), R = 3: ;

2) Определите координаты центра и радиус сферы, если она задана уравнением ;

3) Напишите уравнение сферы с центром С (0; 0; 0), проходящей через точку M (5; 3; 1).

Решение. Координаты точки M удовлетворяют уравнению сферы; подставляем их в общий вид уравнения:

. Тогда уравнение сферы имеет вид:

№1. 1) Доказать, что приведенное уравнение является уравнением сферы. 2)Найти координаты центра и радиус; г)  

Чтобы доказать 1), нужно привести это уравнение к виду .

Для этого придется воспользоваться методом выделения полного квадрата.

Тогда:   доказано

2)