Формулы  и
и  называются эквивалентными (
называются эквивалентными ( ), если совпадают их таблицы истинности. Для доказательства эквивалентности формул будем пользоваться единообразным методом: непосредственная проверка совпадения функций, образующих правую и левую стороны доказываемого соотношения.
), если совпадают их таблицы истинности. Для доказательства эквивалентности формул будем пользоваться единообразным методом: непосредственная проверка совпадения функций, образующих правую и левую стороны доказываемого соотношения.
Пример 1-3. Доказать эквивалентность:


| 
| 
| 
| 
|
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 |
 (1 – 3)
(1 – 3)
Аналогично убеждаемся:  . (1 – 4)
. (1 – 4)
 &(
&( (1 – 5)
(1 – 5)
 . (1 – 6)
. (1 – 6)
 (1 – 7)
(1 – 7)
Справедливость этой формулы вытекает из формул (1 – 4) и (1 – 5).
Формулы де Моргана: а)  (1 – 8)
(1 – 8)
|
|
 (1 – 9)
(1 – 9)
2. Аналитическим способом, т.е. на основе формул взаимосвязи между логическими операциями, докажите справедливость ниже приведенных тождеств. Затем с помощью диаграмм Эйлера – Венна подтвердите справедливость этого доказательства; представьте одно из выражений (предварительно его упростив) в базисе элементарных функции. В наборе номеров базисных функции должны фигурировать цифры вашего варианта. Например, для варианта 12 могут быть взяты следующие функции:  ,
,  ,
,  . Недостающие функции отбираются на основе теории классов.
. Недостающие функции отбираются на основе теории классов.
|
|
|
((a | b) | (a ~ b)) | ((c + d)  (d – c)) =((d
(d – c)) =((d  c)
c)  (a – c))
(a – c))  ((a|d) | (d
((a|d) | (d 
 )),
)),
((a 
 )
)  (b – c))
(b – c))  ((a | d) – (b
((a | d) – (b  d)) = ((a | b) | (a +
d)) = ((a | b) | (a +  ))
))  ((c + d)
((c + d)  (d
(d  c)),
c)),
((a  b)
b)  (a + b)) – ((c–d)
(a + b)) – ((c–d)  (c~d)) = ((c
(c~d)) = ((c  a)
a)  (c
(c  b))
b))  ((a
((a  d)
d)  (b
(b  d)),
d)),
((a ~ b) – (a  b))
b))  ((c ~ d)
((c ~ d)  (c – d)) = ((c – a)
(c – d)) = ((c – a)  (c – b)) | ((a
(c – b)) | ((a  d)
d)  (b
(b  d)),
d)),
((a  b)
b) 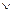 (a + b)) – ((d – c)
(a + b)) – ((d – c)  (d ~ c)) = ((a
(d ~ c)) = ((a  c)
c)  (b
(b  c))
c))  ((a |d) | (b | d)),
((a |d) | (b | d)),
((a  b) – (a + b))
b) – (a + b))  ((c – d)
((c – d)  (c ~ d)) = ((c – a)
(c ~ d)) = ((c – a)  (c – b))
(c – b))  ((a
((a  d) – (b
d) – (b  d)),
d)),
((d  b)
b)  (
( – b))
– b))  ((c
((c 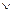 a) | (d
a) | (d  a)) = ((
a)) = (( | d) | (c + d)) | ((a ~b)
| d) | (c + d)) | ((a ~b)  (
( –b)),
–b)),
((a | b) – ( +
+  ))
))  ((d – c)
((d – c)  (c~ d)) = ((
(c~ d)) = ((

 )
)  (b–
(b–  ))
))  ((a
((a  b) – (b–c)),
b) – (b–c)),
((c – a)  (c ~a)) – ((d – b)
(c ~a)) – ((d – b)  (d ~ b)) = ((a
(d ~ b)) = ((a 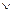 b)
b)  (c
(c  b))
b))  ((d – a)
((d – a)  (c
(c  d)),
d)),
((c ~ b) – (b  c))
c))  ((
(( ~
~  )
)  (a – d)) = ((b
(a – d)) = ((b  d)
d)  (c
(c  d)) | ((a – b)
d)) | ((a – b)  (a – c)),
(a – c)),
((a– d)  (a ~ d)) – ((b – c)
(a ~ d)) – ((b – c)  (b ~ c)) = ((b
(b ~ c)) = ((b  d)
d)  (a | b))
(a | b))  ((c
((c  d) | (a
d) | (a  c)),
c)),
((a  d)
d)  (c
(c  d))
d))  ((a
((a  b) – (a – c)) = ((b
b) – (a – c)) = ((b 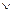 c) – (b + c))
c) – (b + c))  ((a – d)
((a – d)  (a ~ d)),
(a ~ d)),
((c  d) | (c+d)) | ((a~b)
d) | (c+d)) | ((a~b)  (a
(a  b)) = ((a
b)) = ((a 
 )
)  (a–d))
(a–d))  ((b
((b  d)|(b
d)|(b 
 )),
)),
((b  d)
d)  (b
(b  c))
c))  ((d
((d  a) – (c–a))=((c | d) | (
a) – (c–a))=((c | d) | ( ~
~  ))
))  ((a + b)
((a + b)  (b
(b  a)),
a)),
((d – a)  (d ~ a)) – ((c– b)
(d ~ a)) – ((c– b)  (
( +b)) = ((a
+b)) = ((a  b)
b)  (d
(d  b))
b))  ((c
((c  d)
d)  (c – a)),
(c – a)),
((c  d) – (c ~ d))
d) – (c ~ d))  ((a
((a  b)
b)  (a + b)) = ((b
(a + b)) = ((b  c)
c)  (b– d))
(b– d))  ((a | c) – (a – d)),
((a | c) – (a – d)),
((
 b)
b)  (d
(d  b))
b))  ((a
((a  d) |(a
d) |(a  c))=((c
c))=((c  d) | (c~ d)) |((
d) | (c~ d)) |(( +
+  )
)  (a–b)),
(a–b)),
((a  c)
c)  (b–
(b–  ))
))  ((c
((c  d) – (b – d))=((b | c) | (b ~ c))
d) – (b – d))=((b | c) | (b ~ c))  ((a + d)
((a + d)  (a
(a  d)),
d)),
((b 
 )
)  (
( +d)) – ((a –c)
+d)) – ((a –c)  (a~c))=((
(a~c))=((
 b)
b)  (d
(d  c))
c))  ((a– b)
((a– b) 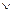 (a
(a  d)),
d)),
((d  a)
a)  (b
(b  d)) | ((a – c)
d)) | ((a – c)  (b–c)) = ((a +
(b–c)) = ((a +  )– (b
)– (b  a))
a))  ((
(( ~
~  )
)  (d– c)),
(d– c)),
((a  b)
b)  (
( ~b))–((c – d)
~b))–((c – d)  (c~d))=((
(c~d))=((
 d)
d)  (
(
 b))
b))  ((c
((c  a)|(c
a)|(c  b)),
b)),
((c  a) – (a+
a) – (a+  ))
))  ((d–b)
((d–b)  (b~d))=((a
(b~d))=((a  b)
b)  (c – d))
(c – d))  ((d
((d  a) – (c
a) – (c  d)),
d)),
задавать функцию алгебры логики. На рис. 1-1 вершины, относящиеся к подмножеству Т1, зачерчены.
 2020-07-12
2020-07-12 211
211








