Модели в пространстве состояний

СЛАЙД 13. Составляя модель объекта на основании физических законов, мы чаще всего получаем систему дифференциальных уравнений первого и второго порядка. Пример, построение модели двигателя постоянного тока на основе применения законов механики и электротехники. Вход этого объекта - напряжение якоря (в вольтах), выход - угол поворота вала (в радианах). Если напряжение питания не меняется, угловая скорость вращения вала двигателя (в радианах в секунду) остается постоянной, при этом угол равномерно увеличивается. Пока вращающий момент двигателя будет равен моменту сопротивления (нагрузки), скорость вращения остается постоянной и ее производная равна нулю. Чем больше напряжение, тем быстрее вращается вал.

Угловая скорость вращения вычисляется как производная от угла поворота вала , то есть (1)

(1)

Соответственно, угол - это интеграл от угловой скорости. В механике уравнение вращательного движения обычно записывают в виде (2):

, (2)

где - вращающий момент, - момент нагрузки (возмущение, также в Н⋅м). Буквой обозначен суммарный момент инерции якоря и нагрузки. В нашем случае момент электромагнитный момент (3)

, (3)

где -коэффициент, -магнитный поток, создаваемый обмоткой возбуждения (измеряется в веберах); -ток якоря (в амперах), который может быть найден из уравнения (4):

, (4)

где - электродвижущая сила (ЭДС) якоря (в вольтах) и - сопротивление якорной цепи (в омах). В свою очередь, ЭДС рассчитывается через магнитный поток и частоту вращения (5):

, (5)

где - коэффициент.

Вводя новые постоянные и , можно записать модель двигателя в виде системы уравнений (6):

. (6)

Модель (6) описывает связи реальных сигналов в системе, ее внутреннее устройство. Часто нам достаточно знать, как будет реагировать объект на заданный входной сигнал (управление). При этом его внутреннее устройство нас не интересует, то есть мы рассматриваем объект в качестве «черного ящика».

СЛАЙД 14. Подставив второе уравнение из системы (6) в третье, найдем и подставим в первое уравнение. Переходя к переменной , получаем (7):

(7)

или, перенося все члены, зависящие от , в левую часть равенства (8)

(8)

Это дифференциальное уравнение второго порядка, связывающее вход и нагрузку с выходом . В сравнении с системой (6), все внутренние сигналы исходной модели ( и ) были исключены из уравнений. Поэтому уравнение (8) называется уравнением «вход-выход».

Порядком модели называют порядок соответствующего дифференциального уравнения. В данном случае мы получили модель второго порядка.

Для того, чтобы было легче исследовать модель объекта, желательно привести ее к некоторому стандартному виду, для которого уже есть готовые общие решения. Таким «стандартом» в теории управления считается система дифференциальных уравнений первого порядка, которая называется нормальной формой Коши.

Рассмотрим снова модель электродвигателя, считая, что (нагрузки нет). Так , можно записать (9) в виде системы (9):

(9)

Эта система дифференциальных уравнений первого порядка в матричной форме(10):

(10)

Значения и определяют состояние двигателя в момент времени t. Это значит, что зная их значения в некоторый момент времени и входной сигнал при всех можно рассчитать поведение объекта для любого последующего момента. При этом предыдущие значения , и (при ) не играют никакой роли. Поэтому и назы ваются переменными состояния, а вектор вектором состояния.

СЛАЙД 15. В ТАУ принято обозначать вектор состояния через 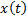, а вход объекта (сигнал управления) через . Тогда модель (9) может быть записана в виде (11):

(11)

где , ,

Уравнение (14) связывает вход и вектор состояния , поэтому она называется уравнением вход-состояние. Здесь 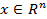– вектор состояния, n – порядок объекта; – вектор управляющих воздействий, ; A – квадратная матрица действительных коэффициентов; B – прямоугольная матрица действительных коэффициентов. Уравнения (15) называют дифференциальным уравнением состояния.

Полная модель объекта в пространстве состояний содержит еще одно уравнение - уравнение выхода, которое показывает, как формируется выход объекта 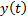: (12)

(12)

– вектор выхода; – прямоугольная матрица действительных коэффициентов. Уравнения (12) описывают линейный многоканальный объект.

Эта модель называется моделью вход-состояние-выход. Выходная координата для двигателя постоянного тока - это угол поворота вала (13):

, (13)

где C = [1 0] и D = 0.

С помощью модели (13), изменяя матрицы C и D, можно принять за выход любую линейную комбинацию переменных состояния и входа. Во многих практических задачах выход - это одна или несколько переменных состояния, которые мы можем измерить.

Поскольку момент инерции J, сопротивление якоря R и коэффициенты и не зависят от времени, матрицы , B, C и D в модели (12) - постоянные. Такие объекты называются стационарными, в отличие от нестационарных объектов, параметры которых изменяются во времени.

Запись моделей в единой форме (12) позволяет отвлечься от смысла переменных состояния и исследовать системы разной природы стандартными методами, которые хорошо разработаны и реализованы в современных компьютерных программах.

Переходная функция

СЛАЙД 16. Один из методов построения моделей «вход-выход» - определение реакции объекта на некоторый стандартный сигнал. Один из простейших сигналов - так называемый «единичный скачок» («единичный ступенчатый сигнал»), то есть мгновенное изменение входного сигнала с 0 до 1 в момент 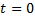. Формально этот сигнал определяется так (1):

(1)

На слайде. Реакция объекта на единичный скачок называется переходной функцией и обозначается :

При этом предполагается, что объект в начальный момент находится в состоянии покоя, то есть, имеет нулевые начальные условия. Это значит, что все его переменные состояния равны нулю и внутренняя энергия также нулевая.