Условие канонической сопряженности можно выразить с помощью скобок Пуассона. Для этого докажем общую теорему об инвариантности скобок Пуассона по отношению к каноническим преобразованиям.
Пусть  – скобка Пуассона величин, в которой дифференцирование производится по переменным
– скобка Пуассона величин, в которой дифференцирование производится по переменным 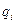 и
и 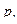 ,
,  - скобка Пуассона тех же величин, дифференцируемых по каноническим переменным
- скобка Пуассона тех же величин, дифференцируемых по каноническим переменным 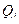 и
и 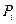 . Тогда
. Тогда
 (9)
(9)
В справедливости этого соотношения можно убедиться прямым вычислением с использованием формул канонического преобразования. Можно, однако, обойтись и без вычислений с помощью следующего рассуждения.
Прежде всего замечаем, что в канонических преобразованиях время играет роль параметра. Поэтому, если мы докажем теорему для величин, не зависящих явно от времени, то она будет верна и в общем случае. Рассмотрим теперь чисто формальным образом величину  как гамильтонову функцию некоторой фиктивной системы. Тогда согласно определению скобок Пуассона
как гамильтонову функцию некоторой фиктивной системы. Тогда согласно определению скобок Пуассона
|
|
|

Но производная  есть величина, которая может зависеть лишь от свойств движения (нашей фиктивной системы) как такового, а не от того либо иного выбора переменных. Поэтому и скобка Пуассона не может измениться при переходе от одних канонических переменных к другим.
есть величина, которая может зависеть лишь от свойств движения (нашей фиктивной системы) как такового, а не от того либо иного выбора переменных. Поэтому и скобка Пуассона не может измениться при переходе от одних канонических переменных к другим.
Из определения скобок Пуассона и теоремы (9) получим:


 (10)
(10)
Это - записанные с помощью скобок Пуассона условия, которым должны удовлетворять новые переменные, для того чтобы преобразование было каноническим.
Интересно отметить, что изменение величин 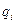 и
и 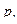 при самом движении можно рассматривать как канонические преобразования. Смысл этого утверждения состоит в следующем. Пусть
при самом движении можно рассматривать как канонические преобразования. Смысл этого утверждения состоит в следующем. Пусть  и
и  – значения канонических переменных в момент времени
– значения канонических переменных в момент времени  , а
, а  и
и  – их значения в другой момент времени
– их значения в другой момент времени  . Последние являются некоторыми функциями от первых (и от величины интервала времени
. Последние являются некоторыми функциями от первых (и от величины интервала времени  как от параметра):
как от параметра):
 ,
, 
Если рассматривать эти формулы как преобразование от переменных  и
и  к переменным
к переменным  и
и  , то это преобразование будет каноническим. Это очевидно из следующего выражения
, то это преобразование будет каноническим. Это очевидно из следующего выражения

для дифференциала действия  , взятого вдоль истинной траектории, проходящей через точки
, взятого вдоль истинной траектории, проходящей через точки  и
и  в заданные моменты времени
в заданные моменты времени  и
и  . Сравнение этой формулы с (6) показывает, что
. Сравнение этой формулы с (6) показывает, что  есть производящая функция преобразования.
есть производящая функция преобразования.
 2020-08-05
2020-08-05 212
212







