Расчет характеристик обнаружения

Вычисление вероятности правильного обнаружения для обнаружителя с постоянным порогом связано с нахождением интеграла от плотности 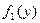. В качестве параметра обнаружения будут использоваться две величины: дефлекция  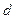и отношение сигнал/шум по мощности .

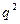Рассмотрим некоторые стандартные задачи обнаружения.

1.    (Сдвиг гауссовского распределения).

В этом случае появление полезного сигнала приводит к сдвигу гауссовской плотности. Если , то вероятность правильного обнаружения равна , где , а  есть интеграл вероятности форме Лапласа. Имеется приближенная граница: , которую можно использовать при .

Нетрудно видеть, что пороговые значения дефлекции, обеспечивающие заданные 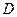 и 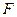, равны . В частности, для ВЛТ  имеем  для  и  для .

Для отношения сигнал/шум по мощности имеем , где . При  получаем .

2.    (Изменение масштаба экспоненциального распределения).

Если при появлении полезного сигнала параметр масштаба увеличивается, т. е. , то можно ввести отношение сигнал/шум по напряжению (дефлекцию) , и получить рабочие характеристики и характеристики обнаружения в аналитическом виде . Вводя обозначения  и , получаем . Таким образом, РХП в координатах 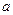 и  получаются в виде прямых линий.

Для фиксированных значени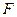й  и 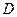 можно вычислить пороговую дефлекцию .

Введем отношение , которое обычно значительно больше единицы в интересующих нас областях характеристик обнаружения. Оно характеризует требование к качеству обнаружения. В результате имеем .

Переходя к отношению сигнал/шум по мощности, получаем . Для порогового отношения сигнал/шум по мощности имеем .

3.  (Изменение масштаба релеевского распределения)

Считаем, что при появлении полезного сигнала параметр масштаба увеличивается. Тогда РХП имеют тот же вид, что и в предыдущей задаче с заменой параметр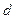а  на 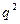. В результате получаем . Сравнивая с предыдущей задачей, можно убедиться, что в данном случае значения порогового отношения сигнал/шум по мощности будут существенно меньшими.

4.    (Шум – логарифмический нормальный, появление полезного сигнала приводит к изменению плотности, которая становится экспоненциальной).

Мощность шума (второй статистический момент) , где  есть отношение математического ожидания к медиане. При появлении полезного сигнала мощность равна .

В данной задаче удобно использовать отношение сигнал/шум по мощности. Поскольку , получаем .

Поскольку вероятность правильного обнаружения , то после подстановки  получаем характеристики обнаружения . Обозначив нормированный к медиане шума порог , получаем, что значение  зависит от требуемой вероятности ложной тревоги и величины . Тогда пороговое отношение сигнал/шум по мощности , где коэффициент  зависит от значения параметра шума , а также от значения вероятности ложной тревоги .

Расчеты показывают, что значение  больше единицы, поэтому пороговое отношение сигнал/шум по мощности в случае логарифмического нормального шума превышает аналогичное отношение сигнал/шум по мощности для экспоненциального шума. Таким образом, коэффициент  отражает потери в пороговом отношении сигнал/шум по отношению к задаче .

5.  (Шум - логарифмический нормальный, появление полезного сигнала приводит к изменению плотности, которая становится релеевской).

Аналогично предыдущей задаче получаем РХП . Пороговое отношение сигнал/шум по мощности . В данном случае коэффициент  отражает потери в пороговом отношении сигнал/шум по мощности по сравнению со случаем релеевского шума, т. е. по сравнению с задачей .

6.  (Шум имеет распределение Вейбулла с некоторыми параметрами, а при появлении сигнала распределение изменяется на релеевское).

В этом случае удобно ввести отношение сигнал/шум по мощности, которое определяет связь параметров ,  и : . Пороговое отношение сигнал/шум определяется по формуле , где нормированный порог , а коэффициент  отражает потери (или выигрыш) а пороговом отношении сигнал/шум по мощности по отношению к задаче .

1.5 Обнаружители с адаптивным порогом при неизвестных параметрах фона

В случае неизвестных характеристик шумового поля возникают трудности в установке порога обнаружения. Незнание характеристик фона и их возможные изменения приводят к тому, что необходимо формировать адаптивный (переменный) порог обнаружения. Для этого обычно используются опорные шумовые выборки с соседних элементов изображения.

Общий алгоритм обнаружения включает три основные процедуры:

1) группирование анализируемых (сигнальных) и опорных (помеховых) каналов,

2) формирование порогов для анализируемых элементов,

3) сравнение и принятие решения.

Процедура группирования связана с выбором формы и размеров скользящих окон для одновременной обработки сигналов, определением числа анализируемых и опорных элементов в пределах выбранных окон, организацией порядка считывания всего изображения при его обработке в процессе обнаружения.

При последовательном считывании изображения организуется скользящее окно, включающее  элементов. При этом полагается, что сигнал может одновременно появиться в  элементах, а остальные 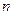 элементов заняты шумовым полем. В процессе считывания каждый из элементов в тот или иной момент оказывается в группе анализируемых.

В лабораторной работе предлагается набор нескольких квадратных сигнальных окон: и ряда помеховых окон. Сигнальное окно располагается в центре помехового. Считывание изображения осуществляется в процессе перемещения скользящего помехового окна (внутри которого находится сигнальное) слева направо вдоль каждой строки с последовательным просмотром строк сверху вниз.

Опорные шумовые выборки используются для оценивания неизвестных параметров шума в анализируемых элементах изображения.

Обычно выбор формы и размеров окна учитывает свойства пространственной однородности или изотропности шумового поля. Для полностью однородного и изотропного шумового поля помеховое окно должно включать все имеющиеся шумовые выборки.

Пусть сигнальное окно содержит  выборок , а помеховое – 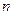 выборок . Обнаружение полезного сигнала производится путем сравнения решающей статистики  (результат формирования сигнала) с порогом : - сигнал есть.

В общем случае адаптивный порог  зависит от всех значений анализируемых и помеховых выборок. Если сигнальное окно содержит только один элемент, т. е. , то алгоритм обнаружения принимает вид .

Математический синтез оптимального алгоритма обнаружения сигнала по выборкам  и  возможен при существовании статистического описания классов  и  для совместных распределений и  при гипотезах  (сигнал есть) и  (сигнала нет). Задача облегчается в случае взаимной независимости выборочных значений помехи между собой и с анализируемой выборкой, а также однородности помехи (одинаковости распределений) в опорных и анализируемых каналах.

Критерий Неймана-Пирсона предусматривает синтез алгоритма, обеспечивающего максимальную вероятность правильного обнаружения  при ограничении вероятности ложной тревоги  на уровне , т. е. .

В параметрической постановке задачи обнаружения классы распределений  и  задаются с помощью аналитического (параметрического) описания плотностей вероятности независимых выборок ,  и , где  и  неизвестные параметры, входящие в выражения для плотностей.

В простейших моделях число компонент, входящих в  и , т. е. число неизвестных параметров, невелико (один-два), что существенно уменьшает трудности синтеза и анализа получающихся алгоритмов. В случае одного полезного (связанного с появлением сигнала) и нескольких мешающих параметра решение задачи упрощается, если существуют достаточные статистики  и , , …,  для этих параметров.

Оптимальный алгоритм в классе несмещенных (у которых вероятность правильного обнаружения не меньше вероятности ложной тревоги) имеет так называемую структуру Неймана , где пороговая функция  находится из уравнения: , включающего условную плотность вероятности  для решающей статистики  при фиксированном значении . Данный алгоритм обладает ценным свойством стабилизации вероятности ложной тревоги на уровне  при изменениях мешающих параметров (параметров распределения помехи) – свойством подобия.

Алгоритмы оценивания параметров шума и формирования адаптивного порога существенно зависят от вида распределения шума. В данной работе рассматривается шум с экспоненциальным распределением, который имеет единственный параметр масштаба. Этот параметр является существенным, поскольку он входит в выражение для вычисления постоянного порога обнаружения. Он также весьма сильно влияет на характеристики обнаружения, т. е. является значимым.

Для экспоненциальных распределений ,  и , с неизвестными параметрами масштаба в результате синтеза равномерно наиболее мощного (РНМ) несмещенного алгоритма получается так называемый "Cell-Averaging Detector" ("CA-Detector" – обнаружитель с усреднением по ячейкам): , где  – положительная постоянная, зависящая от числа помеховых выборок .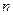

Пороговая функция в данном случае пропорциональна выборочному среднему  с коэффициентом пропорциональности , который обеспечивает заданную вероятность ложной тревоги . Решающая статистика  формируется как выборочное среднее анализируемых выборок .

Приведем выражения для характеристик обнаружения этого адаптивного алгоритма. При независимых одинаково распределенных выборках помехи вероятность ложной тревоги не зависит от параметра масштаба распределения и равна . Отсюда , а пороговый коэффициент равен .

Значение вероятности ложной тревоги будет отличаться от расчетного в случае неоднородной помехи (изменения параметра масштаба в пределах окна), а также при зависимых выборках помехи.

Алгоритм "CA-Detector" можно представить в виде , где . Заметим, что  есть наилучшая оценка неизвестного параметра масштаба  экспоненциального распределения помехи.

В случае известного параметра  оптимальный порог равен , где . Сравнение значений  и , соответствующих одинаковым вероятностям ложной тревоги показывает, что  всегда больше . Это объясняется флуктуациями выборочного среднего , что требует увеличения порога.

При появлении полезного сигнала параметр масштаба увеличивается , где  – дефлекция или отношение сигнал/шум по напряжению, является одновременно относительным изменением параметра масштаба. Если рассматривать увеличение мощности , где , , то отношение сигнал/шум по мощности равно , причем .

При неизвестном параметре масштаба помехи и использовании "СА-Detector" в случае единственной анализируемой выборки (т. е. сигнальное окно содержит один элемент ) характеристики обнаружения определяются выражением . Пороговая дефлекция равна  и зависит от числа опорных выборок помехи.

В непараметрической постановке задача синтеза может формулироваться как проверка идентичности распределений всех (независимых) выборок:

для любых значений .

хотя бы для одной пары  и .

Последняя строчка означает, что выборка  «статистически больше» выборки .

В этом случае процедура обнаружения основывается на использовании знаковых и ранговых статистик, получаемых из вариационного ряда . Например,   есть максимальное значение, а выборочная медиана  вычисляется по формулам:  при ,  при .

Непараметрические статистики обладают достаточной устойчивостью характеристик при изменениях вида распределения независимых опорных выборок, что обеспечивает стабильный уровень вероятности ложной тревоги для алгоритма "Max-Detector" , а также для алгоритма "Med-Detector" . Однако они представляют практический интерес при большом количестве независимых опорных выборок 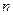, поскольку значения вероятности ложной тревоги имеют порядок . В частности, для алгоритма "Max-Detector" (выбор наибольшего значения для порога) вероятность ложной тревоги равна  при любых распределениях независимых выборок помехи.

При не очень больших 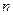 (например, несколько десятков) используются квазинепараметрический вариант алгоритма "Max-Detector" , который позволяет получать требуемые низкие значения вероятности ложной тревоги, за счет выбора постоянной . Эти значения остаются стабильными в классе распределений помехи с единственным неизвестным параметром масштаба. Изменения вида распределения требуют изменения значения порогового коэффициента 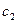, который зависит также от числа выборок 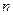. Тем не менее, последний алгоритм более устойчив к отклонениям от принятой модели распределения помехи, чем алгоритм "CA Detector".

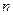Для экспоненциальных моделей вероятность правильного обнаружения, соответствующая алгоритму "Max-Detector" при  вычисляется по формуле , где  – число сочетаний из  по .

Вероятность ложной тревоги получается из этого выражения при . Легко убедиться, что при выборе пороговой константы  алгоритм "Max-Detector" становится чисто непараметрическим и обеспечивает постоянную для любых распределений шума вероятность ложной тревоги .