Метод наибольшего правдоподобия

Метод наибольшего правдоподобия, или алгоритм максимального правдоподобия обеспечивает при отсутствии информации о стоимостях и априорных вероятностях принятия решения принятие той из гипотез, которой соответствует бóльшее значение функции правдоподобия выборки [20, с. 330]. Этот метод можно рассматривать как частный случай метода минимального риска. Алгоритм максимального правдоподобия совпадает с оптимальным алгоритмом по критерию максимума апостериорной вероятности в том случае, когда гипотеза и альтернатива равновероятны. Поэтому граничной значение x ₀ определяется из условия минимума ошибки без учета априорных вероятностей и стоимостей принятия решений следующим выражением:

(11.1)

Этот метод преобразуется из метода минимального среднего риска при условии, что потери при совершении ошибки обратно пропорциональны вероятности их совершения. При этом величина отношения правдоподобия выбирается таким образом, чтобы минимизировать сумму вероятностей ошибок.

Правило решения принимается следующим:

, если	(11.2)
, если ,

где x – значение параметра для диагностируемого объекта.

Граничное значение х = х ₀находится из условия

(11.3)

Сопоставляя условия (9.5) и (11.3), легко установить, что они совпадают, если положить

(11.4)

В большинстве практических случаев используется условие (9.10), и тогда для метода наибольшего правдоподобия следует считать

(11.5)

Для задач надёжности вероятность неисправного состояния обычно представляет собой малую величину, но цена пропуска дефекта значительно больше цены ложной тревоги .Тогда условие (11.5) даёт решение, не требующее знания точных значений стоимости ошибок и качественно отражающее указанные обстоятельства

Пример

Задача. Диагностика механизма осуществляется по температуре подшипниковых узлов. Установлено, что для исправного состояния среднее значение x подшипникового узла составляет 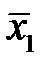=50°C и среднее квадратичное отклонение σ ₁=15°C. При наличии повышенного износа 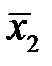=100°C, σ ₂=25°C. Распределения предполагаются нормальными.

Определить предельное значение x ₀, рассчитать вероятность ложной тревоги, вероятность пропуска дефекта и средний риск

, , , .

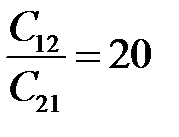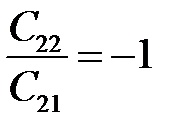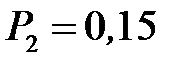Решение. Так как сумма вероятностей исправного и неисправного состояний равна 1, то

По методу наибольшего правдоподобия из (11.3) имеем условие:

Подставив полученные плотности распределения в формулу выше, получим квадратное уравнение относительно х = х ₀:

Подставим известные значения и решим уравнение

Это уравнение имеет положительный корень x ₀= 72,4364°C.

Проведём проверку:

Теперь найдём вероятность ложной тревоги и пропуска дефекта:

Далее найдём средний риск по формуле (9.1):

На рис. 11.1 приведены графики функций плотности вероятности, а также вероятности принятия решения P (x) (вероятность ошибки без учёта априорных вероятностей): Рис. 11.1

Рис. 11.1. Плотности распределения вероятностей и функция вероятности принятия решения P (x) без учёта априорных вероятностей

Выводы.

В результате расчёта по методу наибольшего правдоподобия получили предельное значение диагностического параметра x ₀= 72,436°C, выше которого исследуемый объект подлежит снятию с эксплуатации. При этом вероятность ложной тревоги составляет Р_ЛТ = 0,0573, вероятность пропуска дефекта Р_ПД = 0,0203. Найдена величина среднего риска, которая составляет
R = – 0,064 C ₂₁.

Контрольные вопросы

1. Каков критерий метода наибольшего правдоподобия?

2. Каким образом осуществляется расчёт предельного значения?

3. Каким образом учитываются стоимости?

4. Каким образом учитываются априорные вероятности?

Метод минимакса

Метод минимакса или минимаксный алгоритм [20, c.328] предназначен для ситуации, когда отсутствуют предварительные статистические сведения о вероятности диагнозов D ₁и D ₂. Рассматривается «наихудший случай», т.е. наименее благоприятные значения P ₁и P ₂, приводящие к наибольшему значению (максимуму) риска. Минимаксный критерий является частным случаем критерия Байеса, который обеспечивает минимизацию максимально возможного риска.

Предположим, что величина риска зависит от x и P ₁ (вероятность второго диагноза P ₂ = 1 – P ₁). Из соотношения (9.1) вытекает, что

(12.1)

Для нахождения экстремума приравниваем нулю частные производные по x и P ₁.

Условие

(12.2)

даёт

(12.3)

Из соотношения

(12.4)

получаем

(12.5)

Теперь требуется определить значения x ₀ и P ₁, удовлетворяющие уравнениям (12.3) и (12.5). Если x^* ₀ и P^* ₁ являются корнями указанных уравнений, то точка R (x ₀^*, P ₁^*) является экстремальной.

Можно показать для одномодальных распределений, что величина риска становится минимаксной (т.е. минимальной среди максимальных значений, вызванных «неблагоприятной» величиной P₁). При P ₁ = 0и P ₂ = 1риск принятия ошибочного решения отсутствует, так как ситуация не имеет неопределённости. При P ₁ = 0(все объекты неисправны) из условия (9.5) вытекает и все объекты действительно признаются неисправными; при P ₁=1 и P ₂=0 и в соответствии с имеющейся ситуацией все объекты классифицируются как исправные.

Для промежуточных значений 0< P ₁<1 риск возрастает и при P ₁ =P^* ₁становится максимальным. Рассматриваемым методом выбирают величину x₀ таким образом, чтобы при наименее благоприятных значениях P₁ потери, связанные с ошибочными решениями, были бы минимальными.

Рассмотрим процедуру решения уравнений (12.3) и (12.5). Сначала из уравнения (12.5) найдём значение x^* ₀, что можно сделать следующим образом. Представим уравнение (12.5) в виде

(12.6)

где

(12.7)

Последнее равенство можно записать с помощью функций распределения

(12.8)

Для определения х ₀ уравнение (12.6) решаем по методу Ньютона, связывающему исходные x _{0(n -1)} и последующие x _0(n) приближения

(12.9)

Значение производной

(12.10)

В качестве первого приближения можно принять , где – средние значения x для распределения f (x/D ₁) и f (x/D ₂). При достаточной близости x _0(n)и x _{0(n -1)}принимаем x^* ₀ =x _0(n). Далее из равенства (12.3) находим наименее благоприятное значение вероятностей исправного P^* ₁ и P^* ₂ неисправного состояний

(12.11)

Величину риска определяем по равенству (12.1) при значениях x ₀ =x^* ₀, P ₁ =P^* ₁. Отметим некоторые случаи, в которых решение становится достаточно наглядным. Положим, что условные выигрыши отсутствуют C ₁₁= C ₂₂=0, а цены ошибок одинаковы C ₁₂= C ₂₁. Тогда из уравнения (12.5) вытекает

или ,

где f (x/D ₁) и f (x/D ₂) – соответствующие функции распределения.

Последнее соотношение показывает равенство условных вероятностей ошибочных решений. Рис. 8.1

На рисунке 8.1 для этого случая площади Р_ЛТ и Р_ПД равны.

В общем случае

(12.12)

Зависимость (12.12) выражает равенство условных рисков ошибочных решений. С помощью функции распределения она записывается в виде

(12.13)

Пример

Задача. Диагностика механизма осуществляется по температуре подшипниковых узлов. Установлено, что для исправного состояния среднее значение подшипникового узла составляет 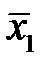=50°C и среднее квадратичное отклонение σ ₁=15°C. При наличии повышенного износа 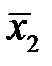=100^оC, σ ₂=25°C. Распределения предполагаются нормальными.

, , , .

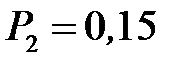Решение. Так как сумма вероятностей исправного и неисправного состояний равна единице, то

По методу минимакса основные соотношения имеют вид (12.3), (12.8), (12.10):

,
, .

Решаем уравнение методом Ньютона путём приближений (12.9) с учётом следующих соотношений:

, , ,

Первое приближение х = х ₀определяем как среднее арифметическое:

Выполняя следующие итерации по (12.9), получим:

, ,

, , .

Прекращение флуктуаций величины x _0(n) после пятой итерации позволяет найти корень уравнения, который равен x ₀= 57,735°C.

Теперь найдём наиболее неблагоприятное значение вероятностей исправного и неисправного состояний P ₁ и P ₂ согласно (12.11).

, .

Подставив формулу для плотности распределения, найдём вероятность ложной тревоги и пропуска дефекта:

Далее найдём средний риск по формуле:

Рассмотрим крайнюю ситуацию, когда C ₁₂ =C ₂₁ = 1, C ₁₁= C ₂₂=0 и рассчитаем новое предельное значение x ₀

Прекращение флуктуаций величины x _0(n) после третьей итерации позволяет найти корень уравнения, который равен x ₀= 68,75°C.

Теперь найдём наиболее неблагоприятное значение вероятностей исправного и неисправного состояний P^** ₁ и P^** ₂ согласно (12.11).

, .

Найдём вероятности

, ,

, .

Далее найдём средний риск по формуле (9.1):

На рис. 12.1 приведены графики функций плотности вероятности f (x)для исправного D ₁ и неисправного D ₂ состояний, а также функция риска принятия решения R (x): Рис. 12.1

Рис. 12.1. Плотности распределения вероятностей и функция риска R (x)

Выводы.

В результате расчёта по методу минимакса получили предельное значение диагностического параметра x ₀= 57,735°C, выше которого исследуемый объект подлежит снятию с эксплуатации. При этом вероятность ложной тревоги составляет Р_ЛТ = 0,211, вероятность пропуска дефекта – Р_ПД = 0,014, а средний риск пропуска дефекта составляет R = – 0,045 C _21.

При C ₁₂ =C ₂₁ = 1, C ₁₁= C ₂₂=0 предельное значение диагностического параметра есть x ₀ = 68,75°C. Уточнённые вероятности Р ₁ = 0,375, Р ₂ = 0,625, вероятность ложной тревоги Р_ЛТ = 0,0396, вероятность пропуска дефекта Р_ПД = 0,066, а средний риск пропуска отказа R = 0,106 C ₂₁.