Вопросы для самоконтроля

По  теме  «Введение  в  анализ»

1. Числовые множества.

2. Абсолютная величина числа и ее свойства.

3. Определение числовой последовательности, способы ее задания.

4. Свойства числовых последовательностей.

5. Бесконечно малые и бесконечно большие последовательности. Связь между ними.

6. Определение числовой функции, способы ее задания.

7. Свойства функций, классификация функций.

8. Понятие предела функции.

9. Предел функции в точке, на бесконечности.

10. Односторонние пределы.

11. Бесконечно большие и бесконечно малые функции, связь между ними.

12. Теоремы о пределе суммы, разности, произведения, частного функций, степени функции.

13. Методы раскрытия основных неопределенностей при вычислении пределов функции.

14. Первый и второй замечательные пределы.

15. Правила сравнения бесконечно малых функций. Перечислить основные эквивалентности для бесконечно малых функций.

16. Понятие о непрерывности функции.

17. Определение точек разрыва функции и их классификация.

18. Свойства непрерывных функций.

Тема 4. Дифференциальное исчисление функции одной переменной

Производная  функции.  Геометрический  и  механический

Смысл  производной

Рассмотрим функцию . Пусть функция  определена в некоторой окрестности точки . Дадим аргументу  приращение , тогда функция получит приращение .

Определение: Производной функции  в точке  называется предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю, если этот предел существует и конечен.

Производная функции  в точке 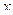 обозначается символами , , . Итак, по определению, .

Рассматривая задачу о проведении касательной к кривой, получили, что , т.е. . Отсюда следует геометрический смысл производной функции . Производная функции  в точке 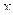 равна угловому коэффициенту касательной в точке  к кривой, заданной уравнением .

Уравнение невертикальной касательной к кривой  в ее точке  можно записать в виде .

Определение: Нормалью к кривой в ее точке  называется прямая, проходящая через точку  перпендикулярно касательной к кривой в этой точке.

В силу условия перпендикулярности двух прямых можно записать уравнение нормали к кривой   в точке  в виде

, если .

Средняя скорость движения на различных промежутках различна. Чем меньше промежуток времени , тем точнее средняя скорость движения «характеризует» это движение в момент времени 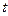. Поэтому предел средней скорости движения при стремлении  к нулю называют скоростью движения точки в данный момент времени 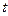 и обозначают

.