Действия над векторами, заданными проекциями

Определение: Тройка векторов , ,  называется координатным базисом, если эти векторы удовлетворяют условиям:

1. вектор  лежит на оси OX, вектор  - на оси OY, вектор  - на оси OZ.

2. каждый из векторов , ,  направлен на своей оси в положительную сторону.

3. векторы , ,  - единичные, т. е.

Рис. 1

Каким бы ни был вектор 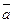, он всегда может быть разложен по базису , , , т. е. может быть представлен в виде , где , ,  - проекции вектора на координатные оси (координаты вектора).

При сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).

 или

 или

или   (2)

При умножении вектора на скаляр координаты вектора умножаются на этот скаляр.

 или

Признаком коллинеарности двух векторов  и  является пропорциональность их координат: .

Задачи

Задача 1. Найти сумму и разность векторов .

Решение: По формуле имеем

 или

 или .

Задача 2. Проверить коллинеарность векторов  и , где , . Установить, какой из них длиннее другого, во сколько раз, как они направлены: в одну или противоположные стороны.

Решение: По формулам находим векторы  и  в координатной форме.

,            ,    

,       ,  

, т. к. , .

Вектор  длиннее вектора  в три раза. Векторы  и  направлены в противоположные стороны (), т. к. .

Лекция № 7 Скалярное произведение двух векторов.

Определение: Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Обозначение скалярного произведения: .

Скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию на него другого.

В результате скалярного умножения двух векторов получается число, скаляр, а не новый вектор.

 

 

Рис. 1

Знак скалярного произведения зависит от угла между векторами.

Замечание. В частности, , если  или .

, если j - острый угол;

, если j - тупой угол;

, если