Прямой чистый изгиб стержня

(к концам стержня приложены только моменты сил)

При прямом чистом изгибе в поперечном сечении стержня возникает только один силовой фактор — изгибающий момент М_х (рис. 18).

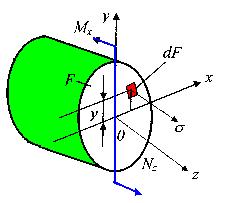
Рис.18. Связь внутреннего усилия и напряжения

Так как Q_y=dM_x/dz=0, то M_x =const и чистый прямой изгиб может быть реализован при загружении стержня парами сил, приложенными в торцевых сечениях стержня. Поскольку изгибающий момент M_х по определению равен сумме моментов внутренних сил относительно оси Ох с нормальными напряжениями его связывает выкающее из этого определения уравнение статики

.

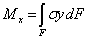Сформулируем предпосылки теории чистого прямого изгиба призматического стержня. Для этого проанализируем деформации модели стержня из низкомодульного материала, на боковой поверхности которого нанесена сетка продольных и поперечных рисок (рис. 19). Поскольку поперечные риски при изгибе стержня парами сил, приложенными в торцевых сечениях, остаются прямыми и перпендикулярными к искривленным продольным рискам, это позволяет сделать вывод о выполнении гипотезы плоских сечений, которая, как показывает решение этой задачи методами теории упругости, перестает быть гипотезой, становясь точным фактом — законом плоских сечений. Замеряя изменение расстояний между продольными рисками, приходим к выводу о справедливости гипотезы о ненадавливании продольных волокон .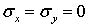

Ортогональность продольных и поперечных рисок до и после деформирования (как отражение действия закона плоских сечений) указывает также на отсутствие сдвигов, касательных напряжений в поперечных и продольных сечениях стержня.

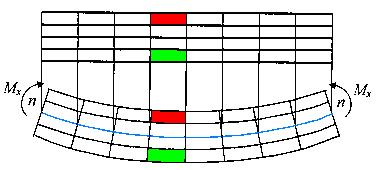
Рис.19. Модель чистого изгиба

Таким образом, чистый прямой изгиб призматического стержня сводится к одноосному растяжению или сжатию продольных волокон напряжениями. При этом часть волокон находится в зоне растяжения (на рис. 19 это – нижние волокна), а другая часть – в зоне сжатия (верхние волокна). Эти зоны разделены нейтральным слоем (п-п), не меняющим своей длины, напряжения в котором равны нулю.

Если J_x —главный центральный момент инерции относительно оси Ох, для кривизны нейтрального слоя получаем формулу

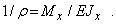
(4)

Кривизна нейтрального слоя 1/r является мерой деформации стержня при прямом чистом изгибе. 1/r тем меньше, чем больше величина EJ_х, называемая жесткостью поперечного сечения при изгибе (по аналогии с жесткостью поперечного сечения при растяжении EF).

Подставляя (4) в (2), получаем формулу для нормальных напряжений в виде

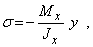
(5)

которая была впервые получена Ш. Кулоном в 1773 году. Для согласования знаков изгибающего момента М_х и нормальных напряжений 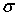в правой части формулы (5) ставится знак минус, так как при M_х>0 нормальные напряжения 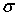при y >0 оказываются сжимающими. Однако в практических расчетах удобнее, не придерживаясь формального правила знаков, определять напряжения по модулю, а знак ставить по смыслу. Нормальные напряжения при чистом изгибе призматического стержня являются линейной функцией координаты у и достигают наибольших значений в волокнах, наиболее удаленных от нейтральной оси (рис. 20), т. е.

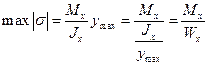
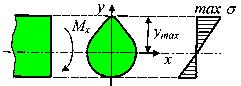
Рис.20. Распределение нормальных напряжений

Здесь введена геометрическая характеристика 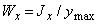, имеющая размерность м³ и получившая название момента сопротивления при изгибе. Поскольку при заданном M_х напряжения 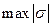тем меньше, чем больше W_x, момент сопротивления является геометрической характеристикой прочности поперечного сечения изгибе. Приведем моменты сопротивления для простейших форм поперечных сечений.

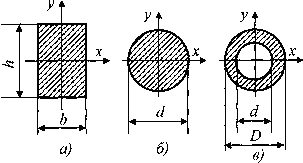
Рис.21. Конфигурации поперечных сечений бруса

Для прямоугольного поперечного сечения (рис. 21, а) имеем:

J_х=bh³/12, y_max = h/2; W_x = J_x/y_max = bh²/6.

Аналогично для круга (рис. 21 ,б):

J_x =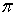 d⁴ /64, y_max=d/2; W_x = 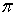d³ /32,

для кругового кольцевого сечения (рис. 21, в):

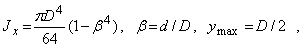
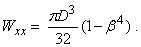
Условие прочности при изгибе балки в форме призматического стержня получает вид

;

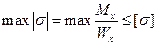где: max M_х— максимальное значение изгибающего момента (легко определяемое по его эпюре), 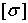— допускаемое напряжение на простое растяжение (сжатие). Напомним, что чистый изгиб балки сводится к растяжению и сжатию ее волокон (неравномерному в отличие от деформации растяжения (сжатия) призматического стержня, при котором ).

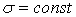Замечание.

Моменты инерци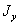и и 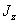всегда положительны, как суммы положительных слагаемых, центробежный же момент

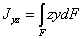
может быть и положительным и отрицательным, так как слагаемые zydF могут быть разного знака в зависимости от знаков z и у для той или иной площадки. Значит, он может быть равен нулю.

Оси, относительно которых центробежный момент инерции обращается в нуль, называются главными осями инерции. Если начало такой системы помещено в центре тяжести фигуры, то это будут главные центральные оси. Эти оси мы будем обозначать 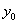и 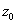; для них .

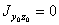Справка по теории моментов: https://www.baurum.ru/alldays/?cat=dynamics-solid&id=3895