Лекция 9
Способ вспомогательных сфер.
 В тех случаях, когда:
В тех случаях, когда:
1. пересекаются две поверхности вращения (L х D = а =?);
2. оси данных поверхностей вращения L и D пересекаются между собой (i x j = О);
3. пересекающиеся оси формируют плоскость, параллельную одной из плоскостей проекций [Г(i x j) II П 2 ],
при построении линий пересечения а данных поверхностей вращения L и D в качестве посредников возможно применение концентрических сфер S с центром О в точке пересечения осей (О = i x j).
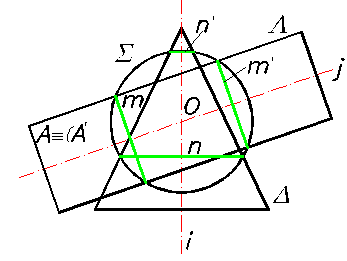
Рис.50 Способ основан на том, что поверхность вращения пересекается с сосной сферой по окружностям, плоскости которых перпендикулярны их общей оси вращения. Соосными называются поверхности, оси которых совпадают. Приведенная на Рис. 50 сфера S является одновременно сосной с поверхностью прямого кругового конуса D и кругового цилиндра L. По этой причине поверхности сфера S и конуса D пересекаются по окружности n, а поверхности сферы S и цилиндра L – по окружности m. Так как обе окружности (m и n)принадлежат одной и той же поверхности сферы S, то, как видно на Рис. 50, они пересекаются между собой в точках A и A. Являясь общими точками для двух пересекающихся поверхностей (D и L), они – эти точки – принадлежат линии пересечения а рассматриваемых поверхностей и L).
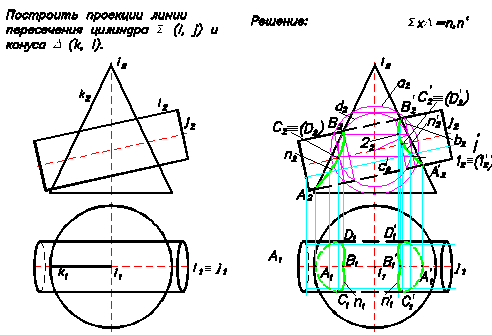 Пример. Построить линию пересечения прямого кругового конуса D и кругового цилиндра S (Рис.51).
Пример. Построить линию пересечения прямого кругового конуса D и кругового цилиндра S (Рис.51).
D х S = n и n' =?
Рис.51
В данном примере:
1. Пересекаются две поверхности вращения (D и S); '
2. Пересекаются оси i и j поверхностей вращения (D и S) соответственно;
i х j = О;
3. Плоскость Г, сформированная пересекающимися осями Г (i х j), параллельна П 2.
Три вышеперечисленные условия являются основанием для применения в качестве посредников концентрических сфер при решении данной задачи.
Сначала определим опорные точки линий пересечения n и n', если таковые имеются. Поскольку плоскость Г является общей плоскостью симметрии обеих пересекающихся поверхностей (D и S), то контурные образующие проекций поверхностей (на плоскости П 2), пересекаясь, (принадлежат одной плоскости Г) определят опорные точки линий пересечения n и n' (A 2, B 2, A' 2и B' 2).
Переходим к определению радиусов минимальной и максимальной сфер.
Rmax равен расстоянию от проекции О 2 до наиболее удаленной точки пересечения очерковых образующих (в нашем случае А 2). Сфера - посредник радиуса Rmax позволит повторно определить точку А. В этом необходимости нет.
Для определения Rmin необходимо из точки О 2 опустить перпендикуляры на очерковые образующие обеих пересекающихся поверхностей (D и S). Больший из них (на Рис.50 к конической поверхности D) и будет Rmin.
Сфера минимального радиуса (d 2 ) коснется конической поверхности D и дважды пересечет цилиндрическую поверхность S. В пересечении проекций полученных окружностей получаем точку 2 (2 2 ), принадлежащую линии пересечения n' (n' 2 ).
Для более точного решения задачи необходимо построить проекции нескольких концентрических сфер с центром в точке О 2 и с радиусами Rmin < Ri < Rmax. На Рис.51 построена проекция а 2 одной из таких сфер. Она пересекает по двум окружностям [одна из них b(b 2)] цилиндрическую поверхность S и по двум окружностям [одна из них c(c 2)] коническую поверхность D. Плоскости этих окружностей ортогональны плоскости проекций П 2 и, соответственно, спроецируется на эту плоскость в виде прямых линий. В пересечениях этих прямых (в2 и с2 ) мы имеем проекции точек 1(1 2 ) и 1'(1' 2 ), которые одновременно принадлежат обеим поверхностям (как принадлежащие линиям этих поверхностей), и, значит, и искомой линии их пересечения n' (n' 2 ).
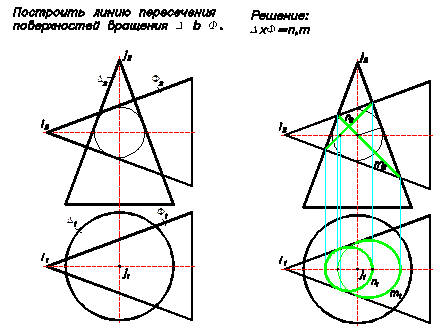 Горизонтальная проекция линии пересечения строится по ее принадлежности конической поверхности.
Горизонтальная проекция линии пересечения строится по ее принадлежности конической поверхности.
 2014-02-05
2014-02-05 1080
1080








