Пределы функций

Определим понятие окрестности точки х ₀ как множество значений х, являющихся решениями неравенства 0<| x - x ₀| < δ, где δ > 0 – некоторое число. Само значение х ₀ может включаться в окрестность или не включаться в нее (в этом случае окрестность называется проколотой).

Пусть функция у = f(x) определена в некоторой окрестности точки х ₀.

Определение 13.7. Число А называется пределом функции у = f(x) при х, стремящемся к х ₀, если 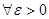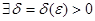такое, что | f(x) - A | < ε при | x - x₀ | < δ.

Обозначение: .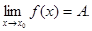

Замечание. Для существования предела функции в точке х ₀ не требуется, чтобы функция была определена в самой этой точке.

Примеры.

1. Докажем, что 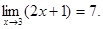Если |2 x +1-7| < ε, то |2 x - 6| < ε, | x - 3| < ε/2. Таким образом, если принять δ(ε) = ε/2, то выполнены все условия определения предела. Утверждение доказано.
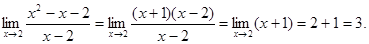2. Заметим, что в проколотой окрестности х=2 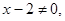поэтому мы имеем право сократить дробь на (х - 2).

Определение 13.8. Функция у = f(x) имеет бесконечный предел при х, стремящемуся к х ₀ (стремится к бесконечности, является бесконечно большой), если 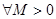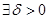такое, что | f(x)| > M при | x - x₀ | < δ.

Обозначение: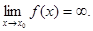

Определение 13.9. Число А называется пределом функции y = f(x) на бесконечности, если 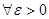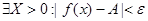при x > X (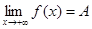), при x < -X (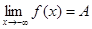), при |x| > X (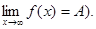

Замечание. Бесконечный предел функции на бесконечности можно определить по аналогии с определением 13.8.

Определение 13.10. Функция у = f(x) называется ограниченной в некоторой области значений х, если существует число М >0 такое, что | f(x)|<M для всех значений х, принадлежащих рассматриваемой области.

Свойства пределов.

1.Если существует 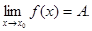(А – конечное число), то функция у = f(x) является ограниченной в некоторой окрестности (возможно, проколотой) точки х ₀.

Доказательство. Так как для любого ε существует такое δ, что | f(x) - A | < ε при | x - x₀ | < δ, то при этом | f(x)| < |A | + ε, то есть функция ограничена в рассматриваемой окрестности.

2. Функция не может иметь двух различных пределов при х, стремящемуся к одному и тому же значению.

Доказательство. Пусть А и В – пределы f(x) при х→х₀. Выберем ε < | A-B |. Тогда существует такое δ₁, что | f(x)-A |<ε/2 при | x - x₀ | < δ₁, и такое δ₂, что |f (x)-B |<ε/2 при | x - x₀ | < δ₂. Если выбрать в качестве δ меньшее из чисел δ₁ и δ₂, то значения функции f(x) для аргументов, лежащих в δ – окрестности х ₀, должны одновременно находиться в двух непересекающихся окрестностях, что невозможно. Утверждение доказано.

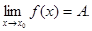1. Если и А 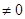, то существует окрестность точки х ₀, в которой функция f(x) сохраняет постоянный знак (f(x)> 0, если A > 0, и f(x)<0, если A < 0).

Доказательство. Достаточно выбрать ε=| A |/2. Тогда для х из некоторой окрестности х ₀ | f(x)-A | < | A |/2, то есть А /2 < f(x) < 3 A /2 при A > 0 и 3 A /2 < f(x) < A /2 при A < 0. Следовательно, в выбранной окрестности f(x) сохраняет постоянный знак.