Применение теории определителей к решению и исследованию систем линейных уравнений
 Рассмотрим систему трех уравнений:
Рассмотрим систему трех уравнений:
| a11 . x1+a12 . x2+ a13 . x3=b1 | |
| a21 . x1+a22 . x2 + a23. x3=b2 | (1) |
| a31 . x1+a32. x2+a33. x3=b3 |
Будем, как в первой лекции, обозначать символами А11, А12, … алгебраические дополнения элементов а11, а12, … определителя
| a11 | a12 | a13 | |||
| D = | a21 | a22 | a23 | (2) | |
| a31 | a32 | a33 |
Умножим обе части первого уравнения системы (1) на А11, второго - на А21, третьего - на А31 и затем почленно сложим эти уравнения:
(a11 . A11 + a21 . A21 + a31 . A31) . x1 + (a12 . A11 + a22 . A21 + a32 . A31) . x2 + (a13 . A11 + a23 . A21 + a33 . A31) . x3 = b1 . A11 + b2 . A21 + b3 . A31
Отсюда и на основании свойств 9 и 10 определителя имеем:
| D. x1 = b1 . A11 + b2 . A21 + b3 . A31 | (3) |
Аналогично найдем:
| D . x2 = b1 . A12 + b2 . A22 + b3 . A32 (4) |
| D . x3 = b1. A13 + b2 . A23 + b3 . A33 (5) |
Правые части уравнения (3), (4) и (5) обозначим соответственно символами 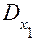 ,
, 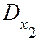 и
и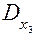 . Тогда эти уравнения примут вид:
. Тогда эти уравнения примут вид:
D . x1= 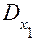 , D . x2=
, D . x2= 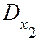 , D . x3=
, D . x3= 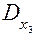 , (6)
, (6)
причем
| b1 | a12 | a13 | |
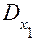 = =
| b2 | a22 | a23 |
| b3 | a32 | a33 | |
| a11 | b1 | a13 | |
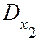 = =
| a21 | b2 | a23 |
| a31 | b3 | a33 | |
| a11 | a12 | b1 | |
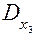 = =
| a21 | a22 | b2 |
| a31 | a32 | b3 |
Определители 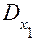 ,
, 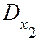 ,
, 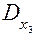 получаются из определителя D в ходе замены соответственно его первого, второго и третьего столбца столбцом свободных членов данной системы.
получаются из определителя D в ходе замены соответственно его первого, второго и третьего столбца столбцом свободных членов данной системы.
Предположим, что D не равно нулю. Из уравнения (6) находим:
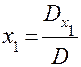
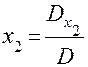
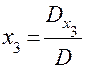 (7)
(7)
Эти формулы называются формулами Крамера. Они определяют решение исходной системы (1). Для доказательства следует подставить в уравнения системы (1) вместо x1, x2, x3 их выражения (7). Убедимся, что, например, первое из них обращается в тождество. Имеем:
a11 . x1 + a12 . x2 + a13 . x3 = a11 . 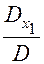 + a12 .
+ a12 . 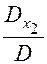 + a13 .
+ a13 . 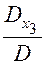 =
=
= 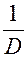 . [ a11 . (b1 . A11 + b2 . A21 + b3 . A31) + a12 . (b1 . A12 + b2 . A22 + b3 . A32) + a13 . (b1 . A13 + b2 . A23 + b3 . A33)] =
. [ a11 . (b1 . A11 + b2 . A21 + b3 . A31) + a12 . (b1 . A12 + b2 . A22 + b3 . A32) + a13 . (b1 . A13 + b2 . A23 + b3 . A33)] =
= 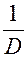 . [ b1 . (a11 . A11 + a12 . A12 + a13 . A13) + b2 . (a11 . A21 + a12 . A22 + a13 . A23) + b3 . (a11 . A31 + a12 . A32 + a13 . A33)]
. [ b1 . (a11 . A11 + a12 . A12 + a13 . A13) + b2 . (a11 . A21 + a12 . A22 + a13 . A23) + b3 . (a11 . A31 + a12 . A32 + a13 . A33)]
Но согласно свойству 9 определителей
a11 . A11 + a12 . A12 + a13 . A13 = D,
а согласно свойству 10
| а11 . А21 + а12 . А22 + а13 . А23 = 0 |
| а11 . А31 + а12 . А32 + а13 . А33 = 0 |
Таким образом,
a11 . 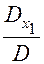 + a12 .
+ a12 . 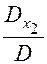 + a13 .
+ a13 . 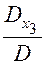 = b1
= b1
Аналогично можно показать, что в тождество обращаются второе и третье уравнения системы.
Приходим к выводу: если определитель D системы (1) отличен от нуля, то существует, и притом единственное, решение этой системы. Оно выражается формулами Крамера (7).
Обобщим изложенное на случай системы n линейных уравнений с n неизвестными. Такая система, определитель которой отличен от нуля, всегда имеет единственное решение. Оно находится следующим образом: значение каждого из неизвестных равно дроби, знаменателем которой является определитель системы, а числитель получится из определителя системы заменой столбца коэффициентов при искомом неизвестном на столбец свободных членов.
Здесь мне снова хочется сказать похвальное слово в адрес моих учениц(ков). В самостоятельную работу №1, которую я упомянул в первой лекции и на которую буду ссылаться в дальнейшем, включено задание на решение системы линейных уравнений по формулам Крамера.
Давайте еще раз насладимся мастерством Лены Гладковой. Вот фрагмент ее решения. Она находит х3 из системы уравнений (пример 1)
 |
| 2x1 + x3 + 4x4 = 9 |
| x1 + 2x2 - x3 + x4 = 8 |
| 2x1 + x2 + x3 + x4 = 5 |
| x1 - x2 + 2x3 + x4 = -1 |
 1. Запишем систему в виде
1. Запишем систему в виде
 2x1 + 0x2 + 1x3 + 4x4 = 9 2x1 + 0x2 + 1x3 + 4x4 = 9
|
| 1x1 + 2x2 - 1x3 + 1x4 = 8 |
| 2x1 + 1x2 + 1x3 + 1x4 = 5 |
| 1x1 - 1x2 + 2x3 + 1x4 = -1 |
2. Найдем
| D = | -1 | |||
| -1 |
3. а) Из элементов первого столбца вычтем удвоенные элементы третьего столбца.
б) Из элементов четвертого столбца вычтем элементы третьего, умноженные на -4.
| D = | -1 | |||
| -3 | ||||
| -3 | -1 | -7 |
4. Разложим этот определитель по элементам первой строки:
| D = | -3 | ||
| -3 | -1 | -7 |
5. К элементам первой строки прибавим элементы третьей строки:
| -2 | |||
| D = | -3 | ||
| -3 | -1 | -7 |
6. Разложим этот определитель по элементам первого столбца:
| -2 | ||||
| D = (-3) . | -3 | = (-3) . (-3+2) = 3 |
7. Находим
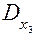 = =
| ||||
| -1 | -1 |
8. а) К элементам первого столбца прибавим элементы второго столбца.
б) К элементам четвертого столбца прибавим элементы третьего.
в) Из элементов третьего столбца вычтем элементы второго.
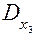 = =
| ||||
| -1 |
9. Разложим этот определитель по элементам четвертой строки:
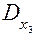 = (-1) . = (-1) .
| = (-3) . | ||||||
10. а) Из элементов первой строки вычтем удвоенные элементы второй.
б) Из элементов третьей строки вычтем элементы второй.
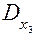 = (-3) . = (-3) .
| |||
| -2 | -3 |
11. Разложим этот определитель по элементам первого столбца:
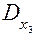 = (-3) . (-1) . = (-3) . (-1) .
| -2 | -3 | = 3 . (-15 + 14) = -3 |
 12. Отсюда: х3 =
12. Отсюда: х3 = 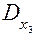 /D =(-3)/3 = -1
/D =(-3)/3 = -1
Вернемся к исследованию системы уравнений (1) и рассмотрим случай, когда ее определитель равен нулю. Здесь возможны два варианта.
1) Если в случае D=0 хотя бы один из определителей 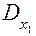 ,
, 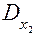 ,
, 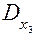 отличен от нуля, то система (1) не имеет решений (говорят, что уравнения этой системы несовместны).
отличен от нуля, то система (1) не имеет решений (говорят, что уравнения этой системы несовместны).
Пример 2. Система
 |
| x1+x2+x3=2 | ||
| 3x1+2x2+2x3=1 | ||
| 4x1+3x2+3x3=4 |
не имеет решений, так как D=0, а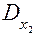 = 1 ≠ 0. В том, что данные уравнения несовместны, видно и непосредственно. Действительно, складывая полученых первые два из них и вычитая полученные результаты из последнего, находим 0=1, т.е. приходим к неправильному неравенству.
= 1 ≠ 0. В том, что данные уравнения несовместны, видно и непосредственно. Действительно, складывая полученых первые два из них и вычитая полученные результаты из последнего, находим 0=1, т.е. приходим к неправильному неравенству.
2) Если D=0 и также 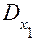 =
= 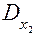 =
= 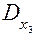 =0, то система (1) либо совсем не имеет решений, либо имеет бесконечно много решений. В последнем случае, по крайней мере, одно из уравнений системы будет следствием других. Такая система называется неопределенной.
=0, то система (1) либо совсем не имеет решений, либо имеет бесконечно много решений. В последнем случае, по крайней мере, одно из уравнений системы будет следствием других. Такая система называется неопределенной.
Пример 3. Система
 x1+x2+x3=1 x1+x2+x3=1
| ||
| 2x1+2x2+2x3=3 | ||
| 3x1+3x2+3x3=4 |
не имеет решений. Даже первые два уравнения этой системы несовместны.
Пример 4. Система
 3x1+x2-x3=1
3x1+x2-x3=1
|
| |
| 5x1+2x2+3x3=2 | ||
| 8x1+3x2+2x3=3 | ||
имеет бесконечно много решений. Видно, что третье уравнение является следствием двух других. Следовательно, данная система равносильна системе двух уравнений с тремя неизвестными.
 |
| 3x1+x2-x3=1 | ||
| 5x1+2x2+3x3=2 | ||
x1, x2 выражаются через х3, а численное значение х3 можно выбрать произвольно.
Однородная система трех линейных уравнений
Линейное уравнение называется однородным, если свободный член этого уравнения равен нулю.
Рассмотрим систему двух линейных однородных уравнений с тремя неизвестными.
 |
| a11 . x1 + a12 . x2 + a13 . x3 = 0 | (8) | |||
| a21 . x1 + a22 . x2 + a23 . x3 = 0 |
1. Если а11/а21 = а12/а22 = а13/а23, то система сводится к одному уравнению, первому или второму, из которого одно из неизвестных выражается через два других, значения которых произвольны.
2. Если условие равенства отношений коэффициентов при неизвестных не выполнено, то решения системы находятся по формулам:
| x1 = | a12 | a13 | . t, | x2 = - | a11 | a13 | . t, | x3 = | a11 | a12 | . t, (9) |
| a22 | a23 | a21 | a23 | a21 | a13 |
где t может принимать любые значения (-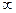 < t < +
< t < + 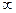 ).
).
Перейдем к рассмотрению системы трех уравнений первой степени с тремя неизвестными:
 |
| a11 . x1 + a12 . x2 + a13 . x3 = 0 | (10) |
| a21 . x1 + a22 . x2 + a23 . x3 = 0 | |
| a31 . x1 + a32 . x2 + a33 . x3 = 0 |
Очевидно, что такая система допускает нулевое решение: x1=0, x2=0, x3=0 и, следовательно, всегда совместна. Если D ≠ 0, то это решение является единственным. Если же определитель однородной системы равен нулю, то возможны два случая, «созвучные» рассмотренным при анализе системы (1).
1) Система сводится к двум независимым уравнениям (третье является их следствием).
2) Система сводится к одному уравнению (остальные два являются его следствиями).
Первый случай имеет место, когда среди миноров определителя системы есть хотя бы один отличный от нуля, второй – когда все миноры этого определителя равны нулю. В обоих случаях однородная система имеет бесчисленное множество решений.
Пример 5. Решить систему
| x1 + 2x2 + 3x3 = 0 |
| 2x1 – 3x2 + 4x3 = 0 |
| 3x1 – x2 + 7x3 = 0 |
 Имеем
Имеем
| D = | = | |||
| -3 | ||||
| -1 |
| = 1 . | -3 | -2. | +3 . | -3 | = -17 – 4 + 21 = 0 | ||||
| -1 | -1 |
 Следовательно, система имеет решения, отличные от нулевого. Решаем систему первых двух уравнений (третье уравнение является их следствием).
Следовательно, система имеет решения, отличные от нулевого. Решаем систему первых двух уравнений (третье уравнение является их следствием).
| x1 + 2x2 + 3x3 = 0 |
| 2x1 – 3x2 + 4x3 = 0 |
Отсюда по формуле (9) получаем:
| x1 = | . t = 17t | ||
| -3 |
| x2 = - | . t = 2t | ||
| x3 = |  . t = -7t . t = -7t
| ||
| -3 |
Второй указанный выше случай имеет место тогда, когда коэффициенты при неизвестных xi пропорциональны, т. е. каждое уравнение системы получается из первого умножением его частей на число k.
Пример 6. Система
 |
| x1 + x2 + x3 = 0 |
| 2x1 + 2x2 + 2x3 = 0 |
| 3x1 + 3x2 + 3x3 = 0 |
имеет бесконечно много ненулевых решений. Она сводится к одному уравнению: х1 + x2 + x3 = 0. Любое решение состоит из трех чисел х1, x2 , x3 , где х1 и x2 - какие угодно, а х3 = - х1 - x2 .
В заключение вспомним известный вам по школьному курсу математики способ решения линейной системы, называемый методом Гаусса. Он состоит в следующем: систему уравнений приводят к эквивалентной ей системе в треугольном виде путем последовательного исключения неизвестных. Эти действия называют прямым ходом. Из полученной «треугольной» системы переменные находят с помощью последовательных подстановок (обратный ход).
Пример 7. Решить систему
| x1 + 2x2 + 3x3 = 2 |
| 2x1 + 3x2 – 4x3 = -5 |
| 3x1 + x2 + x3 = 3 |
 Чтобы исключить х1 из второго и третьего уравнений, надо вычесть из них первое, умноженное соответственно на 2 и на 3:
Чтобы исключить х1 из второго и третьего уравнений, надо вычесть из них первое, умноженное соответственно на 2 и на 3:
 |
| x1 + 2x2 + 3x3 = 2 |
| - x2 – 10x3 = -9 |
| -5x2 – 8x3 = -3 |
Для дальнейших преобразований удобно умножить второе и третье уравнения на -1:
 x1 + 2x2 + 3x3 = 2 x1 + 2x2 + 3x3 = 2
|
| x2 + 10x3 = 9 |
| 5x2+ 8x3 = 3 |
Видим, что для исключения x2 из третьего уравнения, нужно вычесть из него второе, умноженное на 5. В результате получим «треугольную» систему:
 x1 + 2x2 + 3x3 = 2 x1 + 2x2 + 3x3 = 2
|
| x2 + 10x3 = 9 |
| 42x3 = 42 |
 Выполняя обратный ход, с помощью последовательных подстановок, находим неизвестные: x3 = 1, x2 = -1, x1 = 1.
Выполняя обратный ход, с помощью последовательных подстановок, находим неизвестные: x3 = 1, x2 = -1, x1 = 1.
 2014-02-02
2014-02-02 1108
1108








