2014-02-02
497
Уравнение Максвелла в дифференциальной форме имеет вид:
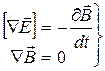Iпара или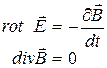 
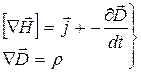II пара или 
К уравнениям добавляют связи:
,
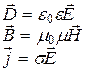где
,
.
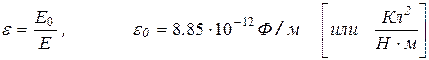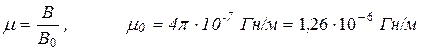Под уравнением волны понимают уравнение вида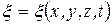 
, где x - смещение точки с координатами x,y,z в момент времени t.
Волна, у которой фронт волны и волновая поверхность являются плоскостями, называется плоской волной.
Её уравнение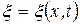 
, где координатная ось X направлена по направлению распространения волны, то есть перпендикулярно волновым поверхностям.
Пусть при x = 0:
.
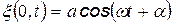Тогда в произвольном значении x колебания придут с запозданием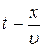 
:
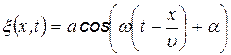
Зафиксировав фазу 
и продифференцировав 
- получим скорость, с которой перемещается данное значение фазы – фазовая скорость.
Учитывая, что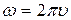 
, 
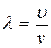, уравнение волны примет вид:
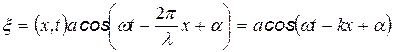
где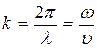 
- волновое число.
Затухание плоской волны, как показа опыт, происходит по экспоненциальному закону
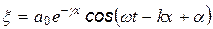
Для точечного источника амплитуда убывает с расстоянием ~1/r даже в непоглощенной среде
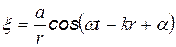
где r – расстояние от точечного источника.
Для волны (плоской) распространяющейся в направлении под углами к осям x, y, z уравнение волны примет вид:
|
|
|
где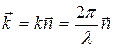 
- волновой вектор
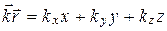
Учитывая, что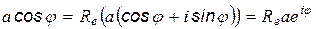 
, уравнение плоской волны можно записать:
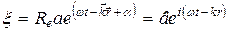
где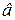 
- комплексное число, называемое комплексной амплитудой, 
.
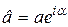Уравнение любой волны является решением дифференцированного уравнения, называемого волновым.
Если продифференцировать функцию дважды по x, y, z, t, сложить производные по координатам и учесть, что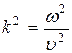 
, получим уравнение, которое называют волновым
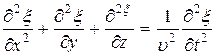
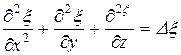
- волновое уравнение
Всякая функция, удовлетворяющая уравнению этого вида, описывает некоторую волну. Корень квадратный из величины, обратной коэффициенту при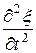 
дает фазовую скорость этой волны.
