Подбор числа базисных функций, каждой из которых соответствует один скрытый нейрон, считается основной проблемой, возникающей при корректном решении задачи аппроксимации, решаемой радиально-базисной сетью. На практике, часто используют два простых алгоритма определения оптимального числа нейронов в скрытом слое. В первом из них происходит увеличение числа нейронов в скрытом слое в процессе обучения сети, начиная с одного. Процесс продолжается до тех пор, пока погрешность обучения не перестанет уменьшаться. Во втором, происходит уменьшение числа нейронов в скрытом слое в процессе обучения сети, начиная с заведомого большого числа нейронов. Процесс также продолжается до тех пор, пока погрешность обучения не перестанет уменьшаться.
Однако, существуют и другме подходы для определения оптимального числа нейронов скрытого слоя.
Семейство сетей RBF является достаточно широким, чтобы равномерно аппроксимировать любую непрерывную функцию на компактном множестве. Теоретический базис построения нейронных сетей на основе радиальных базисных функций дает универсальная теорема об аппроксимации [5].
|
|
|
Пусть 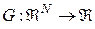 - ограниченная, непрерывная и интегрируемая функция, такая, что
- ограниченная, непрерывная и интегрируемая функция, такая, что
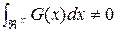 . (4.44)
. (4.44)
Пусть 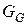 - семейство сетей RBF, включающих функцию
- семейство сетей RBF, включающих функцию 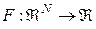 следующего вида:
следующего вида:
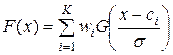 , где
, где 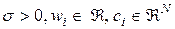 для
для 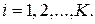 Тогда выполняется следующая теорема об универсальной аппроксимации для сетей RBF.
Тогда выполняется следующая теорема об универсальной аппроксимации для сетей RBF.
Для любой непрерывной функции  найдется сеть RBF с множеством центров
найдется сеть RBF с множеством центров 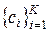 и общей шириной
и общей шириной 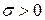 , такая, что функция
, такая, что функция 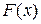 , реализуемая сетью, будет близка к
, реализуемая сетью, будет близка к  по норме
по норме 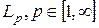 .
.
Теорема является более строгой, чем необходимо для сетей RBF, так как ядро 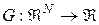 не обязательно должно удовлетворять условию симметрии.
не обязательно должно удовлетворять условию симметрии.
При подборе числа нейронов в скрытом слое приходится учитывать следующие факторы. Слишком малое число нейронов не позволяет сильно уменьшить погрешность обобщения множества обучающих данных, слишком большое число – увеличивает погрешность выводимого решения на множестве тестирующих данных. Как правило, число базисных функций K составляет определенную долю от объема обучающих данных p.
Наиболее эффективным алгоритмом подбора числа скрытых нейронов считается метод ортогонализации наименьших квадратов, использующий алгоритм ортогонализации Грэма-Шмидта [4].
Отправная точка этого метода – представление задачи обучения в виде линейной адаптации вектора весов сети 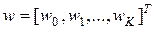 , направленной на минимизацию значения вектора погрешности е. Для p обучающих выборок вектор ожидаемых значений имеет вид:
, направленной на минимизацию значения вектора погрешности е. Для p обучающих выборок вектор ожидаемых значений имеет вид: 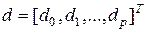 . При использовании К базисных функций и p обучающих пар реакции скрытых нейронов образуют матрицу G вида (4.15)
. При использовании К базисных функций и p обучающих пар реакции скрытых нейронов образуют матрицу G вида (4.15)
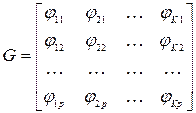 , (4.45)
, (4.45)
в которой 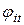 обозначает реакцию i -й радиальной функции на t -ю обучающую выборку,
обозначает реакцию i -й радиальной функции на t -ю обучающую выборку, 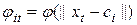 . Если вектор реакций i -й радиальной функции на все обучающие выборки обозначить
. Если вектор реакций i -й радиальной функции на все обучающие выборки обозначить 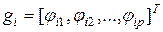 , то матрицу G можно представить в форме
, то матрицу G можно представить в форме 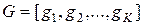 .
.
|
|
|
При таких обозначениях на каждом этапе обучения будет выполняться линейное равенство
 , (4.46)
, (4.46)
где w – вектор весов, а 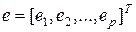 - вектор фактической погрешности обучения. Квадрат произведения Gw соответствует ожидаемой энергии, исходящей от сигналов, задаваемых вектором d, которая и подвергается максимизации в процессе обучения.
- вектор фактической погрешности обучения. Квадрат произведения Gw соответствует ожидаемой энергии, исходящей от сигналов, задаваемых вектором d, которая и подвергается максимизации в процессе обучения.
Метод ортогонализации наименьших квадратов основан на преобразовании векторов g i во множество базисных ортогональных векторов. В процессе обучения матрица 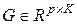 раскладывается на произведение матрицы
раскладывается на произведение матрицы 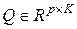 с ортогональными столбцами
с ортогональными столбцами  на верхнетреугольную матрицу
на верхнетреугольную матрицу 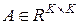 с единичными диагональными значениями:
с единичными диагональными значениями:
G = QA, (4.47)
где 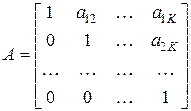 , а матрица Q соответствует условию
, а матрица Q соответствует условию 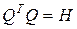 . При этом H – диагональная матрица с элементами
. При этом H – диагональная матрица с элементами 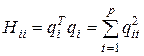 . Решение зависимости (4.35) методом наименьших квадратов может быть спроецировано в пространство, образуемое ортогональными векторами
. Решение зависимости (4.35) методом наименьших квадратов может быть спроецировано в пространство, образуемое ортогональными векторами  . Если ввести новую векторную переменную b, определенную как
. Если ввести новую векторную переменную b, определенную как
b = Aw, (4.48)
то из уравнения (4.35) получим:
d = QB + e. (4.49)
Приближенное решение уравнения (4.38) методом наименьших квадратов имеет вид:
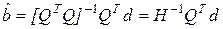 . (4.50)
. (4.50)
Принимая во внимание диагональный характер матрицы Н, можно получить формулу, описывающую i -й компонент вектора 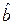 :
:
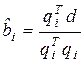 . (4.51)
. (4.51)
Решение, определяющее вектор весов w, находится непосредственно из уравнения (4.37), которое можно переписать в форме 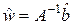 .
.
 2014-02-02
2014-02-02 665
665








