Проектирование условий измерений

Л_13,14

Л_12

Л_11

В этом случае переходят от конечных приращений D_i к средним квадратическим погрешностям m_i следующим образом. Считаем, что каждый из аргументов х_i измерен много раз. В результате этого имеем много различных значений 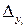. Тогда, возводим в квадрат левую и правую части второго уравнения (3.3.5б) и суммируем. Используя свойство рассеивания случайных величин для функции и аргументов, 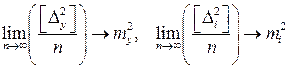и свойство независимости 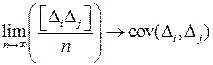, получаем формулу (3.3.5) для некоррелированных результатов измерений.

Таким образом, при одновременном влиянии случайных и систематических погрешностей для оценки точности имеем:

.

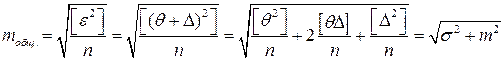Здесь по свойствам случайной величины 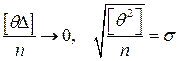– средняя квадратическая систематическая погрешность, но не стандарт, так как для систематических погрешностей не существует свойства рассеивания; 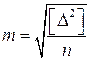– случайная средняя квадратическая погрешность. Несложно показать, что этот же вид будет иметь и оценка точности функции, отягощенная случайными D_i и систематическими погрешностями q_i. Тогда для средних квадратических погрешностей также получим

. (3.3.6)

Здесь m_D – случайная средняя квадратическая погрешность функции из (3.3.2), а m_q – систематическая погрешность функции из (3.3.5б). Считается, что если m_D > 3 m_q (или m_D / m_q > 3), то систематической составляющей можно пренебречь (это равносильно тому, что произведено 171 измерение и искажение точности не более 5%) [10].

Метод взятия полного дифференциала функции (3.3.5) и переход от дифференциалов к средним квадратическим погрешностям используется достаточно часто для поиска погрешностей неявных некоррелированных функций.

Например, 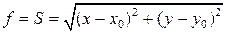, 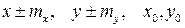– исходные безошибочные координаты. По (3.3.5) имеем

.

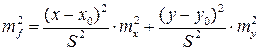Для функции 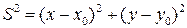полный дифференциал есть

.

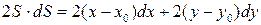Переход к средним квадратическим погрешностям дает

,

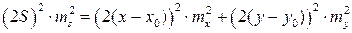или после элементарных преобразований, полученную выше формулу. Если функция представлена как произведение, то возможно прологарифмировав ее и взяв полный дифференциал перейти к средним квадратическим погрешностям: пусть есть функция вида 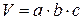, тогда 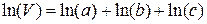, , 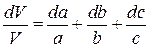переход имеет вид 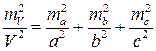– относительная средняя квадратическая погрешность. Отсюда легко получить при необходимости формулу абсолютной средней квадратической погрешности .

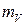Оценка точности вектор – функции. Очень многие геодезические задачи не могут быть описаны одной функцией общего вида, а как минимум двумя и более. В этом случае все они объединяются в вектор-функцию вида

. (3.3.18)

Такого рода структуры, очевидно, не могут быть оценены числом, а только набором чисел. Не сложно понять, что это должен быть набор оценок математических ожиданий (вектор оценок математического ожидания) для каждой функции

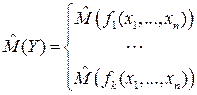(3.3.19)

и набор мер рассеивания для функций 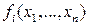, а также меры тесноты связи между ними (если они существуют). Для этого, используя характеристику рассеивания многомерного закона распределения в виде ковариационной матрицы К_Y и расширяя формулу (3.3.2) на k функций (то есть производные берут от каждой из k функций по всем n аргументам), получают обобщенную формулу оценки точности вектор-функции (фундаментальная теорема переноса погрешностей):

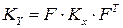, (3.3.20)

где F – матрица Якоби J вида

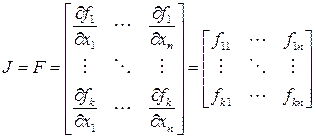, (3.3.21)

а К_х – обычная ковариационная матрица измерений. Формула носит универсальный характер и применима для оценки практически любой вектор-функции вида (3.3.18). При этом, можно показать, что для линейной вектор-функции 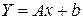(где b как постоянная не влияет на меру рассеивания)

,

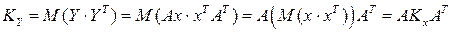а

.

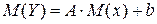Значит (3.3.20) – оценка линеаризованного варианта вектор-функции общего вида и чем больше меры рассеивания аргументов (элементы ковариационной матрицы) тем хуже будет оценка, которую иногда можно улучшить на основе (3.3.4).

Примеры. Рассмотрим некоторые примеры использования формулы оценки точности вектор-функции. Пусть надо оценить среднюю квадратическую погрешность пункта Р, полученного из полярной засечки с не безошибочными исходными координатами. В этом случае имеем вектор-функцию Y

,

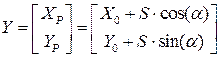и матрицу Якоби F размера 2х4 (две функции X_P, Y_P и четыре аргумента по которым берут производные – X₀, Y₀, S и a)

.

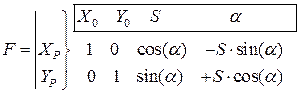Ковариационная матрица для вектор-функции Y

.

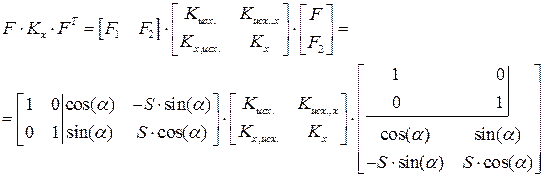Здесь К_исх. – ковариационная матрица погрешностей исходных данных. Если они считаются по отношению к измерениям достаточно малыми, то К_исх = 0 и в матрице F не будет производных по исходным координатам (X₀, Y₀). Если нет, то эта матрица может быть задана в виде полной матрицы обычного вида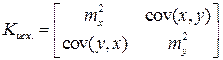– известной из предыдущих вычислений в сети, или неполной 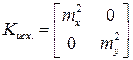– известной из оценки точности при уравнивании опорной сети. Не диагональные блоки матрицы исходных данных К_исх,х или известны из вычислений, или (что чаще всего) равны нулю. К_х – обычная ковариационная матрица измерений. Если исходные данные заданы неполной ковариационной матрицей К_исх, К_х – диагональная матрица измерений, блоки К_исх,х нулевые, то ковариационная матрица вектор-функции будет

.

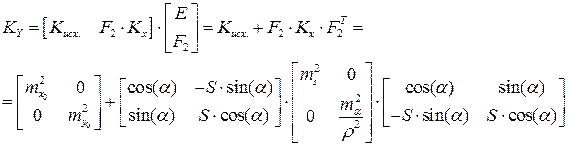Погрешность определения положения пункта вычисляют с использованием круговой погрешности Гельмерта вида

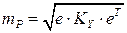, (3.3.22)

где е –вектор-строка из единиц, .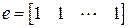

Тогда для нашей задачи имеем

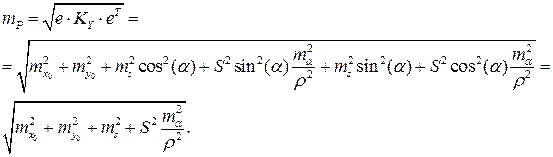
Следует иметь ввиду, что в ковариационной матрице измерений К_х, при разнородных измерениях (например, линии и углы) погрешность измерения углов обязательно переводят в радианы: 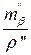чтобы все размерности у слагаемых совпадали (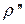– число секунд в радиане равная 206264.8062²» 206265²)

Частный случай формулы Гельмерта (и наиболее известный), при безошибочных исходных данных и диагональной ковариационной матрице, через погрешности приращений есть

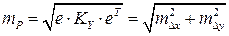. (3.3.22а)

Для полярной засечки это полученная выше формула с диагональными элементами ковариационной матрицы измерений К_х: .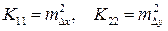

Обратная задача теории погрешностей измерений. Предельное проектирование точности одной функции. Предрасчет точности вектор-функции. Примеры.

Обратная задача теории погрешности измерений. Наряду с прямой задачей теории погрешности измерений – оценки точности функции по погрешностям аргументов, очень большое значение имеет задача предрасчета условий измерений таким образом, чтобы оценка функции (вектор-функции) была или в заданных пределах или оптимальной по какому-либо критерию. Такого рода задачи называют задачами проектирования измерений или априорного предрасчета точности. При этом, первый вариант – получения заданных значений, называют предельным (лимитированным) проектированием, а проектирование с получением наилучших значений – оптимальным проектированием. Из условий измерений, подлежащих регулировке можно выделить следующие факторы: точность измерений, состав измерений, количество измерений, внутренняя геометрия измерений, наличие или отсутствие систематической погрешности (крайне редко), то есть только средства и методы измерения.

Предельное проектирование точности одной функции. Рассмотрим задачу предельного проектирования точности одной функции, которая ставится следующим образом: пусть задана функция 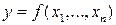(или результат косвенного измерения) и задана ее погрешность m_f. Предрассчитать (спроектировать) условия измерений так, чтобы при их реализации мы получили именно заданную величину погрешности функции. Для этого запишем формулу оценки точности функции (3.3.2) и проанализируем ее:

.

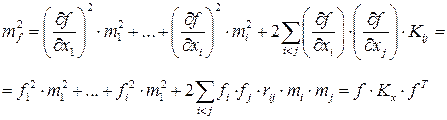Очевидно, что в одном уравнении более одного неизвестного (например, n погрешностей m_i при проектировании по точности) и решение задачи невозможно без привлечения дополнительной информации об условиях измерений. Из всех возможных вариантов такого рода дополнительной информации наибольшее распространение получил принцип взвешенных влияний с равными условиями. По нему недостаток информации компенсируется предположением о равном влиянии на конечный результат каких либо частей в выражении (3.3.2) и введением коэффициентов влияния (весов) этих слагаемых.

Например, пусть (3.3.2) имеет вид

– одно уравнение с тремя неизвестными. Тогда недостаток информации (в две единицы) можно компенсировать введением степени влияния каждого из трех слагаемых в виде чисел 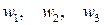, сумма которых равна единице и, обязательно, предположением, что, например, каждое слагаемое, или его часть, вносит примерно одинаковый вклад в формирование значения величины погрешности m_f. Теперь для заданной погрешности функции из

,

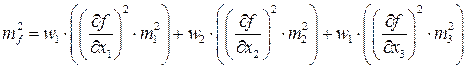и, например, предположения, что 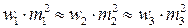, имеем

.

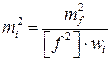Очевидно, что возможно взвешивание приемлемых различных частей слагаемых. Если примерно известны коэффициенты корреляции, то на этой основе также возможно решение задачи, но оно будет более трудоемким. Самая большая проблема в этой постановке, это поиск соответствующих чисел влияния w_i. В принципе они могут быть назначены достаточно произвольно, сообразуясь с постановкой задачи, но в этом случае существует реальная угроза того, что предрассчитанные погрешности m_i будет невозможно реализовать существующими средствами измерений. Очень часто в процессе проектирования, числа влияния игнорируются, а используется только второе предположение о равенстве, или, назначают равные числа влияния не используя второе предположение совсем. Последний подход получил название «принцип равных влияний» и используется более широко, чем другие.

При этом для (3.3.2) возможны следующие варианты равного влияния частей слагаемых:

1. Пусть предполагается, что все погрешности измерений примерно одинаковы 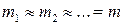. Тогда

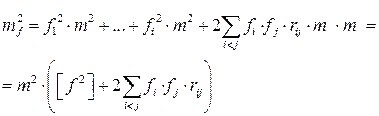
откуда

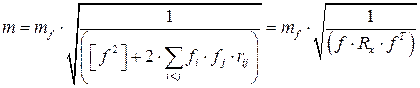, (3.4.1)

где R_x – корреляционная матрица результатов измерений, полученная из ковариационной матрицы K_x.

Приравнивать между собой возможно и элементы структуры f_i, при известных погрешностях измерений m_i. Такого рода проектирование называют проектированием геометрии оцениваемого процесса. Тогда по аналогии имеем

,

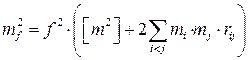откуда аналогично (3.3.23)

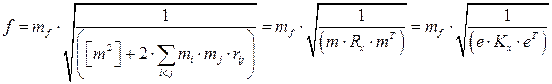. (3.4.2)

Здесь т – вектор-строка погрешностей измерений; К_х – ковариационная матрица измерений; е – вектор-строка из п единиц (сумматор). Здесь учтено, что R_x = D × K_x × D, где D – диагональная матрица с элементами 1/ m_i (масштабатор). Тогда К_х = D ^-1× R_x × D ^-1.

Следует учесть, что f – численное значение частной производной. Таким образом, проектирование здесь возможно только по количественному значению измеренных величин.

Например, пусть при погрешности измерения сторон в квадрате m_a = m_b = 0.1м и сторонах а = b = 10м имеем погрешность определения площад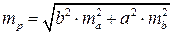и

и .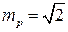

Какие длины должен иметь квадрат, чтобы погрешность площади теперь была т_р= т_y = 1. По (3.4.2) имеем

;

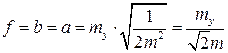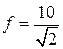
Таким образом, при уменьшении стороны в 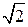раз, погрешность будет заданной величины. Такого рода проектирование целесообразно для примерно одинаковых точностных и геометрических условий.

2. Предположим, что в (3.3.2) одинаковое влияние оказывает произведение вида 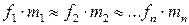. Тогда

,

,

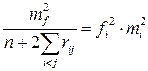откуда значения погрешностей измерений

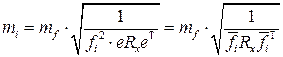. (3.4.3)

Здесь 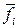– вектор-строка из п одинаковых частных производных f_i.

Если и m_i известны, то из (3.4.3) проектирование по количественному значению (геометрии) будет

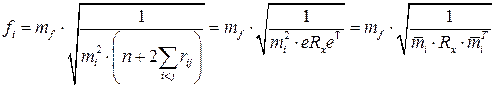, (3.4.4)

где 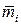– вектор-строка из п одинаковых погрешностей m_i.

Эта формула более гибкая чем (3.4.2), так как позволяет проектировать, в какой то мере, «индивидуальную» геометрию, как и (3.4.3) «индивидуальные» точности в зависимости от геометрии.

Например, в рассмотренном выше примере: а = 10м, b = 20м и m_i = 4м², найти т_а и m_b. По (3.4.3) имеем

.

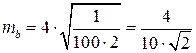
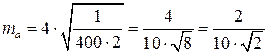Как должны измениться длины, чтобы при этих же точностях измеренийпогрешность площади была равна m_p = 3м². Из (3.4.4) получаем

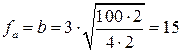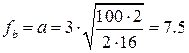м, а м.

Ответ тривиален, но подход может быть использован и в более сложных задачах, например, при оценивании алгоритмов координатоопределения.

3. Пусть теперь приравниваются части вида 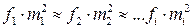. Тогда (3.3.2) примет вид

.

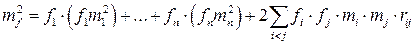Очевидно, что последние суммы нельзя привести к рассматриваемому допущению 3 без дополнительных условий. Поэтому будем рассматривать некоррелированный случай. Исходя из этого (3.3.22) будет

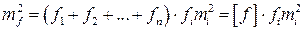. (3.4.5)

Отсюда искомые значения погрешностей

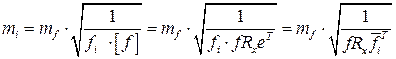, (3.4.6)

где f – вектор-строка из частных производных f_i; 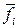– вектор-строка из п одинаковых элементов f_i (см. (3.4.3)).

При проектировании геометрии весьма затруднительно использовать (3.3.2) с третьим условием для выражения значения f_i. Но на основе аналогии с формулами первого и второго условия, формулы (3.4.2), (3.4.4), можно записать

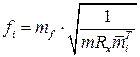. (3.4.7)

Анализ формул показывает, что другие комбинации на основе равных влияний слагаемых или их частей, невозможны. Результаты проектирования сведем в общую таблицу (таблица 3.4.1), из анализа которой также можно сделать этот вывод.

В 2000 году Маркузе М.Ю. [19],был предложен метод степенного взвешивания для проектирования, вида

.

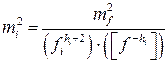Не сложно показать, что при подстановке в (3.3.2) мы имеем тождество, а при h = 0 мы имеем частный случай (3.4.3), h = -1 – (3.4.6), а при h = -2, частный случай формулы (3.4.1). Общий вид проектирования при наличии корреляции по предложенному алгоритму весьма затруднителен, что впрочем не снижает его ценности для практики.