Принцип оптимальности и уравнения Беллмана

Рис. 4.5

Показатель эффективности рассматриваемой управляемой операции — целевая функция — зависит от начального состояния и управления:

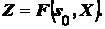(4.9)

Сделаем несколько предположений.

1. Состояние 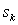системы в конце k- го шага зависит только от предшествующего состояния 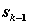и управления на k -м шаге 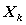(и не зависит от предшествующих состояний и управлений). Это требование называется «отсутствием последействия». Сформулированное положение записывается в виде уравнений

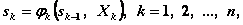(4.10)

которые называются уравнениями состояний.

2. Целевая функция (4.9) является аддитивной от показателя эффективности каждого шага. Обозначим показатель эффективности k -го шага через

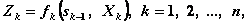(4.11)

тогда

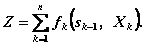(4.12)

Задача пошаговой оптимизации (задача ДП) формулируется так: определить такое допустимое управление X, переводящее систему S из состояния 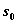в состояние 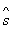, при котором целевая функция (4.12) принимает наибольшее (наименьшее) значение.

Выделим особенности модели ДП:

1. Задача оптимизации интерпретируется как n-шаговый процесс управления.

2. Целевая функция равна сумме целевых функций каждого шага.

3. Выбор управления на k-м шаге зависит только от состояния системы к этому шагу, не влияет на предшествующие шаги (нет обратной связи).

4. Состояние 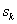после k-го шага управления зависит только от предшествующего состояния 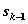и управления 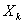(отсутствие последействия).

5. На каждом шаге управление 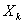зависит от конечного числа управляющих переменных, а состояние 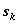— от конечного числа параметров.

Следует вспомнить, что существуют различные способы решения подобных задач, применяемые в зависимости от вида функций, ограничений, размерности и т. п. Рассмотрим вычислительную схему ДП, которая окажется безразличной к способам задания функций и ограничений. Вычислительная схема связана с принципом оптимальности и использует рекуррентные соотношения.

Принцип оптимальности впервые был сформулирован Р. Беллманом в 1953 г. Каково бы ни было состояние s системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный. Беллманом четко были сформулированы и условия, при которых принцип верен. Основное требование — процесс управления должен быть без обратной связи, т.е. управление на данном шаге не должно оказывать влияния на предшествующие шаги.

Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого подпроцесса. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом. Если изобразить геометрически оптимальную траекторию в виде ломаной линии, то любая часть этой ломаной будет являться оптимальной траекторией относительно начала и конца.

Уравнения Беллмана. Вместо исходной задачи ДП с фиксированным числом шагов п и начальным состоянием 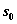рассмотрим последовательность задач, полагая последовательно 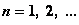при различных 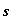— одношаговую, двухшаговую и т.д., используя принцип оптимальности.

Введем ряд новых обозначений. Обозначения в ДП несут большую информационную нагрузку, поэтому очень важно их четко усвоить.

На каждом шаге любого состояния системы 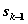решение нужно выбирать «с оглядкой», так как этот выбор влияет на последующее состояние 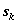и дальнейший процесс управления, зависящий от 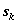. Это следует из принципа оптимальности.

Но есть один шаг, последний, который можно для любого состояния 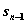планировать локально-оптимально, исходя только из соображений этого шага.

Рассмотрим n-й шаг: 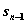- состояние системы к началу n-го шага, 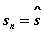- конечное состояние, 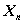- управление на n - омшаге, а 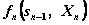— целевая функция (выигрыш) п- гошага.

Согласно принципу оптимальности, 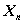нужно выбирать так чтобы для любых состояний 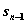, получить максимум целевой функции на этом шаге.

Обозначим через 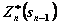максимум целевой функции - показателя эффективности п- гошага при условии, что к началу последнего шага система S была в произвольном состоянии 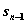, а на последнем шаге управление было оптимальным.

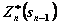называется условным максимумом целевой функции на п-м шаге. Очевидно, что

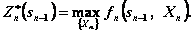(4.13)

Максимизация ведется по всем допустимым управлениям .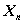

Решение 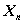, при котором достигается 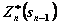, также зависит от 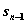и называется условным оптимальным управлением на п-м шаге. Оно обозначается через .

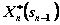Решив одномерную задачу локальной оптимизации по уравнению (4.13), найдем для всех возможных состояний 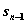две функци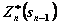и: и .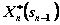

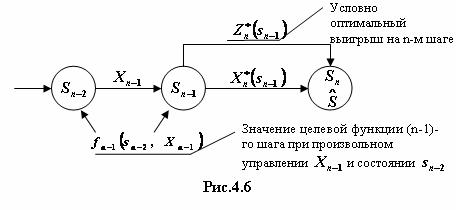
Рассмотрим теперь двухшаговую задачу: присоединим к n-му шагу (n-1)-й (рис. 4.6).

Для любых состояний 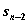, произвольных управлений 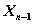и оптимальном управлении на n-м шаге значение целевой функции на двух последних шагах равно:

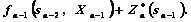(4.14)

Согласно принципу оптимальности для любых 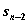решение нужно выбирать так, чтобы оно вместе с оптимальным управлением на последнем (n-м) шаге приводило бы к максимуму целевой функции на двух последних шагах. Следовательно, нужно найти максимум выражения (4.14) по всем допустимым управлениям 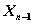. Максимум этой суммы зависит от 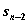, обозначается через 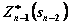и называется условным максимумом целевой функции при оптимальном управлении на двух последних шагах. Соответствующее управление 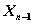на (n-1)-м шаге обозначается через 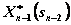и называется условным оптимальным управлением на (n-1)-м шаге.

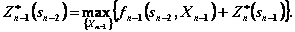(4.15)

Следует обратить внимание на то, что выражение, стоящее в фигурных скобках (4.15), зависит только от 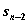и 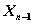, так как 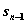можно найти из уравнения состояний (4.10) при к=п -1

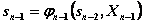
и подставить вместо 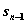в функцию .

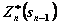В результате максимизации только по одной переменной 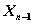согласно уравнению (12.7) вновь получаются две функци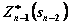и:

и .

Далее рассматривается трехшаговая задача: к двум последним шагам присоединяется (n-2)-й и т. д.

Обозначим через 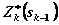условный максимум целевой функции, полученный при оптимальном управлении на п-к+1 шагах, начиная с k-го до конца, при условии, что к началу k-го шага система находилась в состоянии 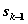. Фактически эта функция равна

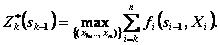
Тогда

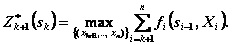
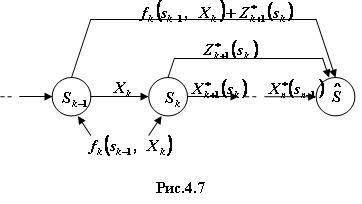
Целевая функция на n-k последних шагах (рис. 4.7) при произвольном управлении на k - мшаге и оптимальном управлении на последующих n-kшагах равна

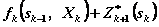Согласно принципу оптимальности, выбирается из условия максимума этой суммы, т.е.

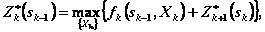(4.16)

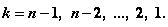
Управление на k-мшаге, при котором достигается максимум в (4.16), обозначается через 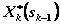и называется условным оптимальным управлением на k-м шаге (в правую часть уравнения (4.16) следует вместо 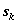подставить выражение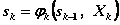, найденное из уравнений состояния).

Уравнения (4.16) называют уравнениями Беллмана. Это рекуррентные соотношения, позволяющие найти предыдущее значение функции, зная последующие. Если из (12.5) найти 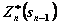. то при k=n-1из (4.16) можно определить, решив задачу максимизации для всех возможных значений 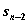, выражения для 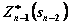и соответствующее . Далее, зная 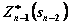, находим, используя (4.16) и (4.10), уравнения состояний.