2014-02-02
571
Если величина средней зависит от всех значений признака, встречаемых в данном распределении, то значение средней определяется структурой распределения, местом распределения.
Медиана – значение признака, приходящееся на середину ранжированной совокупности. Медиана делит совокупность на две равные части.
Пример 6.8. Вес 7 телят: 75, 80, 83, 87, 92, 97, 101 кг.
Медиана равна 87 кг (половина телят имеет вес меньше 87 кг, а половина – больше 87 кг).
Вес 8 телят: 75, 80, 83, 87, 92, 97, 101, 105 кг.
Медиана равна (87+92)/2=89,5 кг.
Медиана в интервальном ряду рассчитывается следующим образом:
Сначала исчисляют порядковый номер медианы по формуле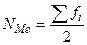 
и строят ряд накопленных частот Si=fi+Si-1 (S1=f1).
Накопленной частоте, которая равна порядковому номеру медианы или первая его превышает, соответствует медианный интервал. Медиана равна:
,
где x0 – нижняя граница медианного интервала;
h – величина медианного интервала;
fi – частота i-го интервала;
Sме-1 – сумма накопленных частот в интервале, предшествующем медианному;
|
|
|
fMe – частота медианного интервала.
Пример 6.9. Имеются данные о заработной плате рабочих:
| Месячная з/п, $ | Количество рабочих, fi | Накопленные частоты, Si |
| до 800 | ||
| 800 – 1000 | ||
| 1000 – 1200 | ||
| 1200 – 1400 | ||
| 1400 и более | ||
| Итого | - |
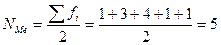, следовательно, медианный интервал 1000-1200.
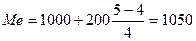$ (половина рабочих имеет заработную плату ниже 1050$, а половина – выше 1050$).
Квартили – значения признака, делящие ранжированную совокупность на четыре равные по числу единиц части.
Номер квартильного интервала рассчитывается аналогично медианному в соотношении ¼ к совокупности. 1-й квартиль равен:
,
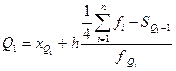xQ1 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%),
h – величина интервала,
fQ1 – частота квартильного интервала,
SQ1-1 – сумма накопленных частот в интервале, предшествующего квартильному.
2-й квартиль:
Q2=Мe.
3-й квартиль:
,
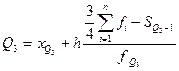обозначения аналогичны 1-му квартилю с изменением на номер интервала.
Пример 6.10. По данным примера 6.9.
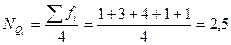, следовательно, 1-й квартильный интервал 800-1000.
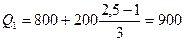$ (25% рабочих получает заработную плату ниже 900$).
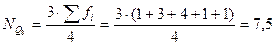, следовательно, 3-й квартильный интервал 1000-1200.
$ (25% рабочих получает заработную плату выше 1175$).
Децили – значения признака, делящие ранжированную совокупность на десять равных по числу единиц частей.
Вычисляются они по той же схеме, что и медиана, и квартили. Обычно рассчитывают только первый и девятый децили:
,
.
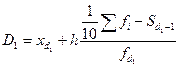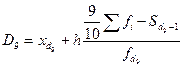Пример 6.11. По данным примера 6.9.
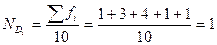, следовательно, 1-й децильный интервал до 800.
$ (10% рабочих получает заработную плату ниже 800$).
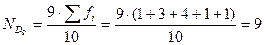, следовательно, 9-й децильный интервал 1200-1400.
|
|
|
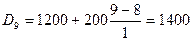$ (10% рабочих получает заработную плату выше 1400$).
Децильный коэффициент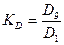 
. Широко применяется при изучении дифференциации доходов.
Пример 6.12. По данным примера 6.11.
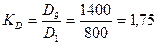(10% самых высокооплачиваемых работников получают зарплату в 1,75 раза больше 10% самых низкооплачиваемых работников).
Мода – значение признака, которое чаще других встречается в изучаемом ряду распределения.
Мода для дискретного ряда определяется как варианта, имеющая наибольшую частоту.
Для интервального ряда:
,
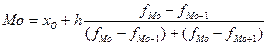где x0 –нижняя граница модального интервала,
d - величина модального интервала,
fMo-1 - частота интервала, предшествующего модальному,
fMo - частота модального интервала,
fMo+1 - частота интервала, следующего за модальным.
Пример 6.13. По данным примера 6.9.
Модальный интервал с наибольшей частотой fi = 4 равен 1000-1200.
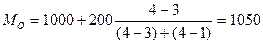$ (наибольшее число рабочих получает зарплату 1050$).
