1). К сферическим координатам целесообразно переходить, когда тело ограничено сферой 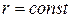 , конусом
, конусом 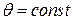 или поверхностью, уравнение которой содержит
или поверхностью, уравнение которой содержит 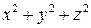 .
.
2). Наиболее удобен порядок интегрирования (слева направо) по 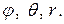
3). Сначала расставить пределы интегрирования по 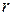 (двигаясь по лучу из начала координат), потом ─ по
(двигаясь по лучу из начала координат), потом ─ по 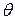 (двигаясь от оси
(двигаясь от оси 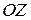 ), потом ─ по
), потом ─ по 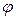 .
.
4). Если уравнение границы области или подынтегральная функция содержат 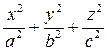 , то следует перейти к обобщенным сферическим координатам
, то следует перейти к обобщенным сферическим координатам
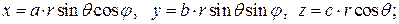 тогда
тогда 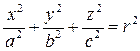 ,
,
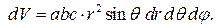
Пример 1. Вычислить момент инерции относительно плоскости 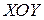 однородного (с плотностью
однородного (с плотностью 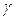 ) тела, ограниченного поверхностями
) тела, ограниченного поверхностями 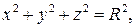
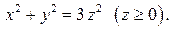
Решение. Момент инерции тела вычислим по формуле
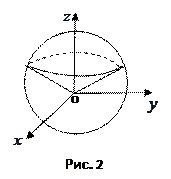
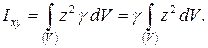
Так кактело ограничено сферой и конусом (рис. 2), то перейдем к сферическим координатам. При этом, учитывая формулы (7.30), уравнение сферы примет вид 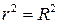 или
или 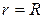 ; уравнение конуса примет вид
; уравнение конуса примет вид
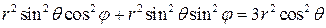 , или
, или 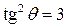 , или
, или 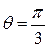 .
.
Используя формулы, получим
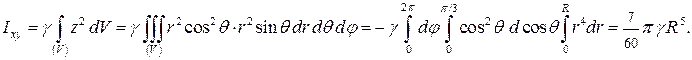
 Пример 2. Найти объем тела, ограниченного поверхностью
Пример 2. Найти объем тела, ограниченного поверхностью
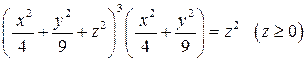 .
.
Решение. Перейдем к обобщенным сферическим координатам
|
|
|
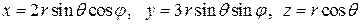 . В этих координатах
. В этих координатах
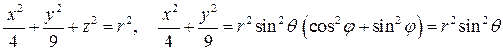
и уравнение поверхности примет вид
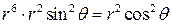 или
или 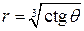 .
.
По условию 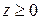 , поэтому
, поэтому 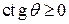 и
и 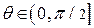 . Cоставим таблицу:
. Cоставим таблицу:
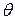
| 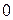
| 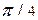
| 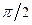
|
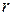
| 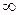
| 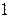
| 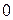
|
Построим точки с вычисленными координатами 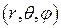 сначала при
сначала при 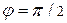 , т.е. в
, т.е. в
плоскости 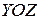 (рис. 3). Так как уравнение поверхности
(рис. 3). Так как уравнение поверхности 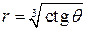 от
от 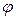 не зависит, то при любом
не зависит, то при любом 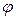 получим такую же линию; все эти линии образуют поверхность вращения (рис. 3). Объем тела, ограниченного этой поверхностью, вычислим с учетом соотношения при
получим такую же линию; все эти линии образуют поверхность вращения (рис. 3). Объем тела, ограниченного этой поверхностью, вычислим с учетом соотношения при 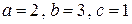 :
:
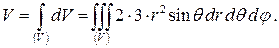
Чтобы расставить пределы изменения 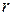 , будем двигаться в области
, будем двигаться в области 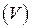 по лучам, выходящим из начала координат. На каждом таком луче
по лучам, выходящим из начала координат. На каждом таком луче 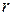 меняется от значения
меняется от значения 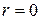 в начале координат до значения
в начале координат до значения 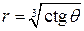 на поверхности, ограничивающей область
на поверхности, ограничивающей область 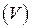 . Кроме того, эта область заключена между лучами
. Кроме того, эта область заключена между лучами 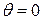 и
и  ,
, 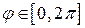 . Поэтому
. Поэтому
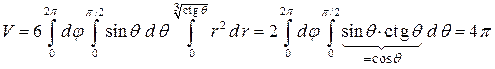 .
.
 2014-02-02
2014-02-02 670
670








