Теорема 19. Если функция 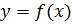 дифференцируема в некоторой точке, то она непрерывна в ней.
дифференцируема в некоторой точке, то она непрерывна в ней.
Доказательство. Пусть функция 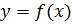 дифференцируема в некоторой точке
дифференцируема в некоторой точке 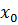 . Тогда существует предел
. Тогда существует предел
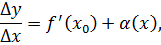
где 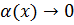 при
при 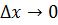 . Отсюда
. Отсюда 
Доказательство.
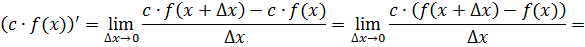
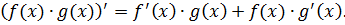
Доказательство.
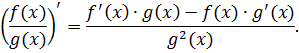
Доказательство.
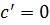 .
.
Доказательство. Пусть 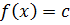 , тогда
, тогда
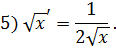 Показательные функции.
Показательные функции.
1) 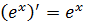 .
.
Логарифмические функции.
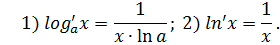
Тригонометрические функции.
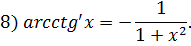
Дифференциал и его геометрический смысл.
Основные понятия.
Пусть функция 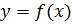 имеет в точке
имеет в точке 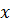 отличную от нуля производную
отличную от нуля производную
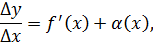
где 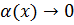 , при
, при 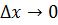 , отсюда
, отсюда 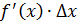 и
и 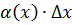 . Величину
. Величину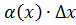 называют главной частью приращения функции
называют главной частью приращения функции 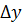 .
.
Дифференциалом функции 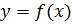 в точке
в точке 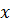 называется главная часть ее приращения в этой точке. Обозначается
называется главная часть ее приращения в этой точке. Обозначается 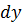 или
или 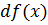 ,
, 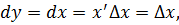
то 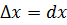 и
и 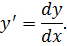
Пример 46. Найти дифференциалы функций 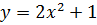 и
и 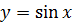 .
.
Решение. Для первой функции 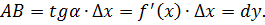
Таким образом, дифференциал функции в точке 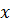 равен приращению ординаты касательной к графику функции в этой точке при приращении аргумента
равен приращению ординаты касательной к графику функции в этой точке при приращении аргумента 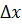 . В этом заключается геометрический смысл дифференциала.
. В этом заключается геометрический смысл дифференциала.
Применение дифференциала к приближенным вычислениям.
Пусть дана функция 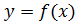 . Тогда
. Тогда 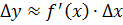 , и
, и 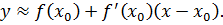
Пример 47. Вычислить приближенное значение 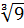 .
.
Решение. Рассмотрим функцию 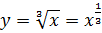 . Пусть
. Пусть 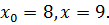 Так как
Так как
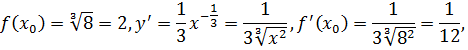
то 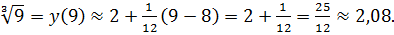
 2014-02-02
2014-02-02 305
305








