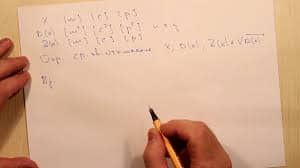Условие монотонности функции

Формула Тейлора для четных и нечетных функций

Теорема 1. Если функция f (x) четна и существует f ^{(2 n+ 1)}(0), то имеет место следующее разложение этой функции

.

Если функция f (x) нечетна и существует f ^{(2 n +2)}(0), то имеет место следующее разложение этой функции

.

Теорема 2. Если функция f (x) четна и существует f ^{(2 n+ 2)}(x)в некоторой окрестности U (0), то для xÎU (0) справедливо равенство

,

где xÎ(0 ,x) или xÎ(x, 0).

Если функция f (x) нечетна и существует f ^{(2 n+ 3)}(xi в некоторой окрестности U (0), то для xÎU (0) справедливо равенство

,

где xÎ(0, x) или xÎ(x,0).

Доказательство. Как уже отмечалось ранее, у четной функции все производные нечетного порядка являются нечетными функциями и, поэтому, они равны нулю с точке

f ^{(2 k+ 1)}(0) = 0, если f (x)четна.

Отсюда и получаются указанные формулы, если использовать многочлен Тейлора до порядка 2 n +1включительно. У нечетной функции все производные четного порядка будут нечетными функциями и

f ^{(2 k)}(0) = 0, если f (x)нечетна.

В этом случае необходимо использовать многочлен Тейлора до порядка 2 n+ 2включительно.

4.6 Исследования характера поведения функций

Исследование функций. Монотонность, экстремумы, выпуклость, точки перегиба, асимптоты.

Теорема 1. Для того, чтобы непрерывная на [ a,b ] и дифференцированная на (a,b) функция f (x) была постоянной на [ a,b ] н. и д., чтобы f¢ (x)º0 на (a,b).

См. следствие теоремы Лагранжа о конечных приращениях.

Теорема 2. Для того, чтобы непрерывная на [ a,b ], дифференцируемая на (a,b) функция f (x) была не убывающей (не возрастающей) на [ a,b ] н. и д., чтобы f¢ (x)³0 (f¢(x) £0) на (a,b).

Доказательство. Необходимость

далее к перейти пределу.

Достаточность. Если x¢ < x¢¢, то по теореме Лагранжа

f (x¢¢) - f (x¢) =f¢ (x)(x¢¢- x¢) откуда и следует требуемая монотонность.

Пример. Оценить погрешность приближения функции sin x многочленом третьей степени на отрезке [0,p/2].

Рассмотрим функцию f (x) = sin x – x +x ³/6.Имеем f¢ (x) = cos x – 1 + x ²/2и далее ³ - 2, на[0, p /2]. Отсюда следует, что функция f (x)монотонно возрастает на указанном отрезке и, таким образом, достигает максимума в точке p /2. max | sin x – x +x ³/6 |= 1 -p/2 + p³/48»0.075.

Теорема 3. Для того, чтобы непрерывная на [ a,b ], дифференцируемая на (a,b) функция f (x) была строго монотонно возрастающей (убывающей) на [ a,b ] н. и д., чтобы f¢ (x)³0 (f¢ (x)£0) на (a,b) и чтобы не существовало промежутка [a,b]Ì[ a,b ], на котором f¢ (x)º0.

Утверждение теоремы является непосредственным следствием теоремы 2.

Следствие. Для непрерывной на [ a,b ], дифференцируемой на (a,b) функции f (x) условие f¢ (x)>0 (f¢ (x)<0) на (a,b) влечет строгое монотонное возрастание (убывание).

Пример. Доказать, что для любого n функция

f_n (x) =x (p /2-arctg nx)строго монотонно возрастает на [0, +¥) и.

f¢_n(x) = - arctg nx – = - g(nx), где g (u) = arctg u +. Имеем g¢ (u)=.

g (0)=0, g (+ ¥)=p/2. Таким образом, g (nx) < p/2и, следовательно, f¢_n (x) = - g (nx) > 0.

Отсюда следует, что Для вычисления последнего предела воспользуемся правилом Лопиталя