Параграф 1.9.3: Моментные функции случайных процессов

Определение n-мерной функции распределения вероятностей при достаточно больших n на практике затруднительно. Однако, большое число задач, связанных с описанием случайных сигналов, удается решать, используя частичное описание случайных процессов, задаваемое моментами тех случайных процессов, которые наблюдаются в сечении этих процессов. Поскольку, в общем случае, эти моменты зависят от временных аргументов, они получили название моментных функций. Для техники связи наибольшее значение имеют моментные функции низших порядков, которые наиболее полно характеризуют случайный процесс. Такими функциями являются математическое ожидание, или среднее значение процесса, определяющееся как:

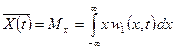
где 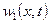– одномерная плотность в сечении t.

Математическое ожидание является одномерной начальной моментной функцией 1 порядка (одномерная, т.к. только для одной функции; 1 порядка, т.к. х – 1 порядка). Математическое ожидание в общем случае является детерминированной функцией времени. Разность межу случайным процессов и его математическим ожиданием, называется центрированным процессом:

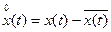(равно 0)

Математическое ожидание квадрата центрированного процесса называется дисперсией:

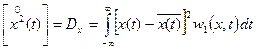
Дисперсия является одномерным (в одном сечении) центральным моментом 2 порядка (усредняется центрированный процесс). Дисперсия позволяет судить о степени разброса мгновенных значений, принимаемых отдельными реализациями в фиксированном сечении. В общем случае, дисперсия так же является детерминированной функцией времени. Величина 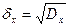называется среднеквадратическим отклонением случайного процесса.

Функция корреляции случайного 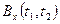определяется как математическое ожидание произведения двух центрированных сечений:

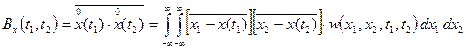
Корреляционная функция представляет собой двумерный (2 сечения) центральный момент 2 порядка. Функция корреляции в общем случае является функций двух моментов времени t₁ и t₂. Она характеризует степень статистической связи отклонений от средних значений (флуктуаций) случайных величин, наблюдаемых при t = t₁ и t = t₂. её называют функцией автокорреляции.

Существует также функция взаимной корреляции между двумя процессами X(t) и Y(t):

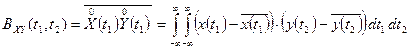
Где 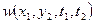– двумерная совместная плотность распределения вероятностей в процессах X и Y в сечении .

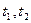Сопоставляя формулы автокорреляции и дисперсии, отметим, что при совмещении дисперсии функции автокорреляции совпадают.

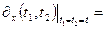
Из формулы для функции автокорреляции также следует, что если значение случайного процесса x(t) в сечениях 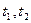взаимонезависимы:

,
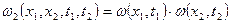то 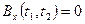(два интеграла в формуле 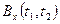в этом случае – это два математических ожидания центрированных случайных процессов).

Наряду с корреляционной функцией для описания случайных процессов применяют ковариационную функцию.

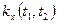– характеризует степень статистической взаимосвязи не флуктуацией, а значение случайной величины в сечении .

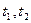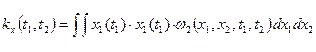– это автоковариационная функция.

Аналогично можно привести формулу взаимоковариационной функции.

В зарубежной литературе используется обратная терминология:

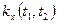– автокорреляционная функция.

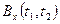– автоковариационная функция.

На практике часто пользуются нормированной корреляционной функцией:

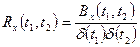– коэффициент корреляции случайного процесса.

При совмещении сечений .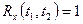

Замечание:

Раздел теории вероятности, посвященный изучению лишь тех свойств случайных процессов, которые определяются рассмотренными в данном пункте характеристиками, и называется корреляционной теорией. Корреляционная теория дает полное описание очень важного класса задач случайных процессов, называемых гауссовскими, и поэтому находит применение при решении большого числа практических задач.