Рис.82
Назначим обобщенной координатой смещение z груза по вертикали от положения равновесия, при котором пружина была растянута на величину 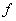 .
.
Тогда потенциальная энергия относительно положения равновесия 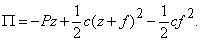 Где
Где 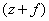 - полная деформация пружины, а
- полная деформация пружины, а 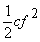 - потенциальная энергия пружины в положении равновесия, которую вычитаем из потенциальной энергии полностью деформированной пружины. Раскрыв скобки, получим
- потенциальная энергия пружины в положении равновесия, которую вычитаем из потенциальной энергии полностью деформированной пружины. Раскрыв скобки, получим
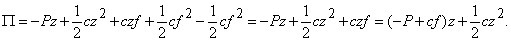
В положении равновесия должно выполняться условие 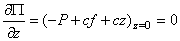 . Отсюда
. Отсюда 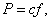 значит,
значит, 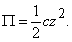
Кинетическая энергия системы
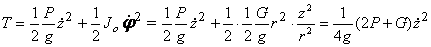
Составив уравнение Лагранжа, получим 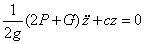 или
или 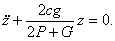 Сравнивая с (6), находим частоту колебаний
Сравнивая с (6), находим частоту колебаний 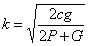 и затем период
и затем период 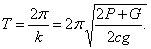
Пример 28. Определим период малых колебаний балочки АВ на цилиндрической поверхности (см. пример 26).
Потенциальная и кинетическая энергии определены. Разложим их в ряд с точностью до малых величин второго порядка. Для этого достаточно положить 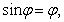 а
а 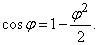 Получим
Получим 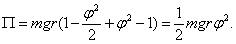 Кинетическая энергия получится такой (отбросив член четвертого порядка -
Кинетическая энергия получится такой (отбросив член четвертого порядка - 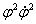 ):
): 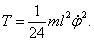
Составляем уравнение Лагранжа. Определив производные
|
|
|
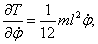
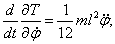
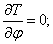
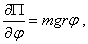 получим уравнение
получим уравнение 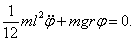 Приводим его к форме (6):
Приводим его к форме (6): 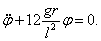 Поэтому частота малых колебаний
Поэтому частота малых колебаний 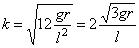 и период
и период 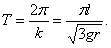
Известно, что свободные колебания не длятся очень долго. Как правило они, как говорят, затухают и довольно скоро. Причиной этому является чаще всего – сопротивление среды, в которой движутся части колебательной системы.
Обычно считают это сопротивление пропорциональным скорости. Пусть на каждую точку материальной системы действует сила сопротивления  Обобщенная сила, соответствующая этим силам,
Обобщенная сила, соответствующая этим силам,
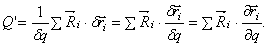
Скорость точек 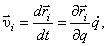 так как
так как 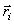 - сложная функция,
- сложная функция, 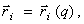 а
а 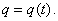 Поэтому
Поэтому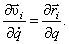 Значит,
Значит,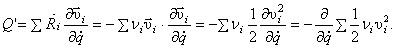
Обозначим  Тогда обобщенная сила сопротивления
Тогда обобщенная сила сопротивления 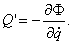
Заметим, что по форме эта функция 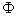 аналогична кинетической энергии Т. Поэтому, если разложить ее в ряд Маклорена и учесть члены лишь второго порядка малости, результат получится тоже аналогичным (5):
аналогична кинетической энергии Т. Поэтому, если разложить ее в ряд Маклорена и учесть члены лишь второго порядка малости, результат получится тоже аналогичным (5): 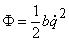 (коэффициент b также будет положительным). И тогда обобщенная сила сопротивления движению
(коэффициент b также будет положительным). И тогда обобщенная сила сопротивления движению
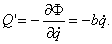 (9)
(9)
Функция 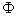 называется диссипативной или функцией рассеивания энергии системы.
называется диссипативной или функцией рассеивания энергии системы.
После подстановки в уравнение Лагранжа 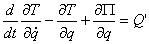 , получим дифференциальное уравнение
, получим дифференциальное уравнение 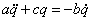 или
или
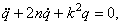 (10)
(10)
где 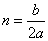 - коэффициент сопротивления,
- коэффициент сопротивления, 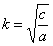 - частота свободных колебаний без сопротивления.
- частота свободных колебаний без сопротивления.
Найдем решение уравнения (10). Характеристическое уравнение: 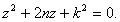 Корни его
Корни его 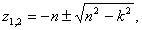 могут быть и комплексными, и вещественными в зависимости от сопротивления, от величины коэффициента n.
могут быть и комплексными, и вещественными в зависимости от сопротивления, от величины коэффициента n.
а) Случай малого сопротивления (n < k).
Корни получаются комплексными 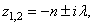 где
где 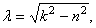
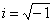 . Решение дифференциального уравнения ищем в виде
. Решение дифференциального уравнения ищем в виде
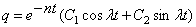 (11)
(11)
или
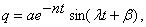 (12)
(12)
где постоянные 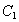 и
и 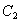 или
или  и
и 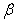 находятся по начальным условиям.
находятся по начальным условиям.
Сравнивая решение (12) с (2), делаем вывод, что это будут колебания, но не гармонические, так как амплитуда колебаний, равная 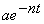 , не постоянная, уменьшается с течением времени. Поэтому такие колебания и называются затухающими.
, не постоянная, уменьшается с течением времени. Поэтому такие колебания и называются затухающими.
|
|
|
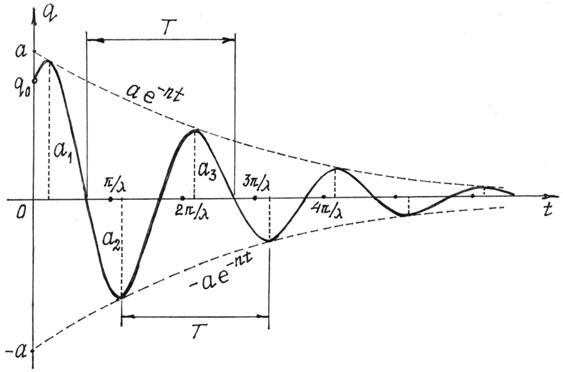
График таких колебаний дан на рис. 83.
 2014-02-03
2014-02-03 958
958








