Рисунок 5
Для стержня круглого сечения (рис. 5, б) путем несложной операции интегрирования можно найти
 .
.
Кроме того,
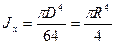 ,
, 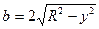 ,
,
откуда
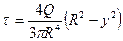
и
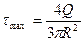
Для стержня, имеющего сечение в форме треугольника с основанием 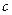 и высотой
и высотой 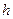 (рис. 5, в), имеем:
(рис. 5, в), имеем:
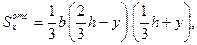
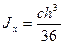
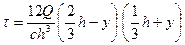 .
.
Максимальное напряжение имеет место на расстоянии 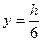 от нейтральной оси:
от нейтральной оси:
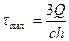
В двутавровых балках касательные напряжения в точках поперечного сечения стенки в месте примыкания ее к полке могут быть значительными, так как статический момент полки относительно нейтральной оси велик, а
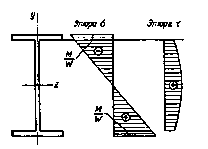
Рисунок 6
толщина стенки даже в очень высоких балках невелика (10...20 мм); это следует из формулы Журавского. В то же время нормальные напряжения в этих точках поперечного сечения лишь немного меньше максимальных (рис. 6). Проверка прочности в подобных случаях расчета двутавровых балок производится с использованием теорий прочности:
Определение главных напряжений при плоском изгибе
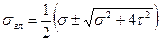 ; (3)
; (3)
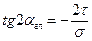 (4)
(4)
Расчетные (эквивалентные) напряжения для полной проверки прочности балок при плоском поперечном изгибе рассчитываются по четырем теориям прочности
|
|
|
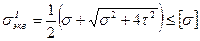 ; (5)
; (5)
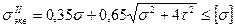 (6)
(6)
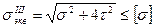 ; (7)
; (7)
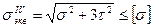 ; (8)
; (8)
Следует заметить, что необходимость в такой дополнительной проверке прочности определяется не только формой поперечного сечения, но и видом эпюр поперечных сил и изгибающих моментов.
Литература
Основная
1. Беляев Н.М. Сопротивление материалов, «Наука», М., 1976г.
2. Дарков А.В., Шпиро Г.С. Сопротивление материалов, «Высшая школа», М., 1975г.
3. Васильев В.З. Краткий курс сопротивления материалов с основами теории упругости, издание «Иван Феодоров», Санкт-Петербург, 2001г.
4. Смирнов А.Ф. Сопротивление материалов, «Высшая школа» М., 1975г.
Дополнительная.
1. Феодосьев В.И. Сопротивление материалов, «Наука», М., 1975г.
2. Таран В.И. Сопротивление материалов. Пособие по решению задач,
издание «Демеу»Алматы, 1992г, 204с.
3. Качурин В.К. Сборник задач по сопротивлению материалов, «Наука», М., 1972г, 430с.
Лекция 14
ТЕМА: ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ
ПЛАН:
15.1 Определение устойчивости
15.2 Критическая сила. Допускаемая нагрузка
15.3 Формула Эйлера
Из теоретической механики известно, что равновесие абсолютно твердого тела может быть устойчивым, безразличным и неустойчивым. Например, шар, лежащий на вогнутой поверхности, находится в состоянии устойчивого равновесия. Если ему сообщить небольшое отклонение от этого положения и отпустить, то он снова возвратится в свое исходное положение (рис. 1,а). Шар, лежащий на горизонтальной поверхности, находится в состоянии безразличного равновесия (рис. 1, б).
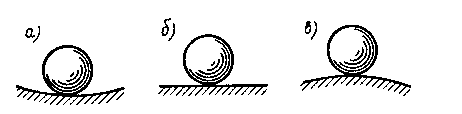 |
Рисунок 1
Будучи отклоненным от этого положения, он в исходное положение не возвращается, но движение его прекращается. Наконец, шар, лежащий на выпуклой поверхности, находится в состоянии неустойчивого равновесия (рис. 1, в). Будучи отклоненным от первоначального положения, он продолжает двигаться дальше.
|
|
|
Аналогичные примеры можно привести и из области равновесия деформирующихся тел.
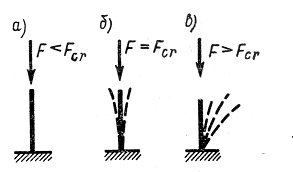 Так, длинный стержень при действии сравнительно небольшой осевой сжимающей силы (меньшей некоторого критического значения) находится в состоянии устойчивого равновесия (рис.2,а).
Так, длинный стержень при действии сравнительно небольшой осевой сжимающей силы (меньшей некоторого критического значения) находится в состоянии устойчивого равновесия (рис.2,а).
Рисунок 2
Если незначительно изогнуть его какой нибудь поперечной нагрузкой и затем эту нагрузку убрать, то стержень вновь распрямится, примет первоначальную форму равновесия.
Искривленная форма равновесия стержня при этом оказывается неустойчивой и потому невозможной.
При значении сжимающей силы, превосходящей определенное критическое значение, наоборот, прямолинейная форма равновесия становится неустойчивой и поэтому сменяется криволинейной формой равновесия, которая оказывается при этом устойчивой (рис. 2,в).
Наименьшее значение сжимающей силы, при котором сжатый стержень теряет способность сохранять прямолинейную форму равновесия, называется критической силой и обозначается Ркр (рис. 2,б).
По определению Эйлера, критической силой называется сила, требующаяся для самого малого наклонения колонны.
Рассмотренная схема работы центрального сжатого стержня носит несколько теоретический характер. На практике приходится считаться с тем, что сжимающая сила может действовать с некоторым эксцентриситетом, а стержень может иметь некоторую (хотя бы и небольшую) начальную кривизну.
Поэтому с самого начала продольного нагружения стержня наблюдается его изгиб.
Исследования показывают, что, пока сжимающая сила меньше критической, прогибы стержня будут небольшими, но при приближении значения силы к критическому они начинают чрезвычайно возрастать (рис. 2,в).
Этот критерий (теоретически неограниченный рост прогибов при ограниченном росте сжимающей силы) может быть принят за критерий потери устойчивости. Практически, стержень разрушится раньше, в результате исчерпания прочности материала.
Определив критическую силу, необходимо установить допускаемую нагрузку на сжатый стержень.
В целях безопасности допускаемая нагрузка, естественно, должна быть меньше критической:
[Р] = Ркр /nу, (1)
где nу – коэффициент запаса устойчивости.
Коэффициент запаса устойчивости принимается таким, чтобы была обеспечена надежная работа стержня, несмотря на то, что действительные условия его работы могут быть менее благоприятны, чем условия, принятые для расчета (из-за неоднородности материалов, неточности в определении нагрузок и т.д.). При этом коэффициент запаса прочности, так как учитываются дополнительные неблагоприятные обстоятельства: начальная кривизна стержня, возможный эксцентриситет действия нагрузки и др.
Для стали нормативный коэффициент запаса устойчивости nу принимается в пределах от 1,8 до 3, чугуна – от 5 до 5,5, для дерева – от 2,8 до 3,2. Указанные значения коэффициентов запаса устойчивости принимаются при расчете строительных конструкций. Значения nу, принимаемые при расчете элементов машиностроительных конструкций (например, ходовых винтов металлорежущих станков), выше указанных; так, для стали принимают nу= 4¸5. Чтобы лучше учесть конкретные условия работы сжатых стержней, рекомендуется применять не один общий коэффициент запаса устойчивости, а систему частных коэффициентов, так же как и при расчете на прочность.
Потеря устойчивости упругого равновесия возможна также при кручении, изгибе и сложных деформациях.
ФОРМУЛА ЭЙЛЕРА
· формула Эйлера
· коэффициент приведенной длины
|
|
|
Влияние способа закрепления концов стержня на критическую силу
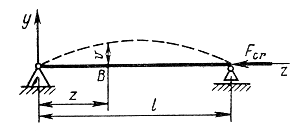 Рассмотрим, сжатый стержень в критическом состоянии, когда сжимающая сила достигла критического значения, т.е. примем, что стержень слегка изогнут (рис. З). Если моменты инерции относительно двух главных центральных осей поперечного сечения не равны между собой, то продольный изгиб произойдет в плоскости наименьшей жесткости, т. е. поперечные сечения стержня будут поворачиваться вокруг той оси, относительно которой момент инерции имеет минимальное значение. В этом легко убедиться, сжимая гибкую линейку.
Рассмотрим, сжатый стержень в критическом состоянии, когда сжимающая сила достигла критического значения, т.е. примем, что стержень слегка изогнут (рис. З). Если моменты инерции относительно двух главных центральных осей поперечного сечения не равны между собой, то продольный изгиб произойдет в плоскости наименьшей жесткости, т. е. поперечные сечения стержня будут поворачиваться вокруг той оси, относительно которой момент инерции имеет минимальное значение. В этом легко убедиться, сжимая гибкую линейку.
Для изучения продольного изгиба и определения критической силы используем приближенное дифференциальное уравнение изогнутой оси балки
Рисунок 3
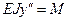 . (2)
. (2)
Изгибающий момент относительно центра тяжести сечения В в изогнутом состоянии
М = - Ркр у. (З)
Знак минус берется потому, что стержень изгибается выпуклостью вверх, а прогиб у положительный. Если бы стержень изогнулся выпуклостью вниз, то момент был бы положительным, но прогибы и были бы отрицательными, и мы снова получили бы тот же результат (З). С учетом (З) уравнение (2) принимает вид
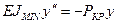 .
.
Обозначая a2 = Ркр / (EJmin), получаем
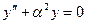 . (4)
. (4)
Это линейное дифференциальное уравнение второго порядка. Его общее решение, как известно из математики, имеет вид
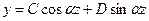 . (5)
. (5)
Здесь С и D — постоянные интегрирования, для определения которых используем известные условия на концах стержня: 1) при z=0, y=0; 2) при z= l, y=0.
Из первого условия получим С=0. Следовательно, стержень изгибается по синусоиде 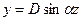 . Из второго условия получим
. Из второго условия получим 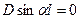 . Это соотношение справедливо в двух случаях.
. Это соотношение справедливо в двух случаях.
1-й случай. D=0. Но если С=0 и D=0, то, как следует из уравнения (5), прогибы стержня равны нулю, что противоречит исходной предпосылке.
2-й случай.  . Это условие выполняется, когда
. Это условие выполняется, когда 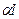 принимает следующий бесконечный ряд значений:
принимает следующий бесконечный ряд значений: 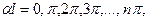 где n — любое целое число. Отсюда
где n — любое целое число. Отсюда 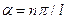 , а так как
, а так как 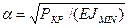 , то
, то 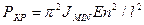 . Таким образом, получается бесчисленное множество значений критических сил, соответствующих различным формам искривления стержня.
. Таким образом, получается бесчисленное множество значений критических сил, соответствующих различным формам искривления стержня.
С практической точки зрения интерес представляет лишь наименьшее значение критической силы, при котором происходит потеря устойчивости стержня.
|
|
|
Первый корень n=0 не дает решения задачи. При n=1 получаем наименьшее значение критической силы:
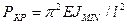 (6)
(6)
Это и есть формула Эйлера.
Критической силе, определяемой по этой формуле, соответствует изгиб стержня по синусоиде с одной полуволной:

Следующие корни дают большие значения критической силы, и мы их рассматривать не будем. Им соответствует изгиб стержня по синусоиде с несколькими полуволнами, который получается в том случае, если изгиб по синусоиде с одной полуволной почему-либо невозможен, например из-за наличия промежуточных связей.
Следует обратить внимание на то, что постоянная D, а следовательно, и форма изогнутой оси стержня остались неопределенными.
Если применить для исследования продольного изгиба не приближенное, а точное дифференциальное уравнение изогнутой оси (см. изгиб, дифференциальное уравнение изогнутой оси балки), то оказывается возможным определить не только значение критической силы, но и зависимость между сжимающей силой и прогибом стержня.
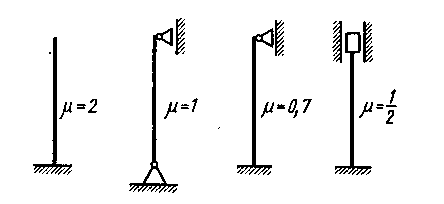 |
Чаще всего концы стержня закрепляют одним из четырех способов, показанных на рис. 4.
Рисунок 4
Второй способ — шарнирное закрепление обоих концов — рассмотрен нами при выводе формулы Эйлера.
При других способах закрепления обобщенная формула Эйлера для определения критической нагрузки имеет вид
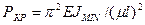 , (7)
, (7)
где m — коэффициент приведенной длины стержня (коэффициент Ясинского), зависящий от способа закрепления концов стержня (рис. 4).
Формула (7) получается, если рассмотреть дифференциальное уравнение продольного изгиба
 ,
,
которое следует из уравнения (4) после двукратного дифференцирования.
 2014-02-13
2014-02-13 3090
3090








