Рассмотрим в начале работу цифрового тракта. 2 страница

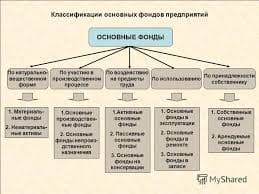
Пусть некоторое событие потока возникло в момент времени t= 0. Запишем вероятность dq (t) появления следующего за ним события потока (одиночного события в силу ординарности потока) на интервале (t, t+dt). Эта вероятность в силу отсутствия последействия не будет зависеть от предыстории потока, т.е. от того, какие значения принимал временной интервал между событиями в прошлом

.

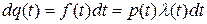Здесь f (t)– плотность вероятности появления события в момент t; p (t) – вероятность отсутствия события на интервале времени (0, t);λ(t)– условная плотность вероятности появления события в момент времени 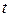при условии, что в предшествующий момент времени оно отсутствовало (интенсивность появления событий).

В результате преобразований, изложенных в разделе 1, и при условии стационарности потока (λ(t) = const) получаем экспоненциальный закон распределения вероятности для p (t) в виде (1.7).

Покажем теперь, что число событий пуассоновского потока, попадающих на любой из интервалов, распределено по закону Пуассона, а именно вероятность попадания на интервал (0, t)ровно
m событий выражается формулой

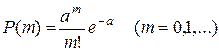, (2.1)

где a – среднее число событий, приходящееся на интервал (0, t). При этом для стационарного пуассоновского потока 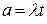, для нестационарного 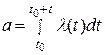и зависит от того, в какой точке начинается рассматриваемый интервал.

Рассуждая по индукции, прежде всего, заметим, что, как следует из вышеизложенного, вероятность отсутствия событий на интервале (0, t) описывается экспоненциальной зависимостью (1.7). Аналогичный результат получается и из выражения (2.1) при m=0, с учетом, что 0!=1. Покажем теперь справедливость выражения (2.1) при m= 1. Пусть единственное событие возникает на интервале времени 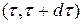(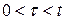). Тогда вероятность его появления определяется выражением

.

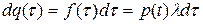Для получения искомой вероятности необходимо проинтегрировать это выражение по всему интервалу (0, t)

.

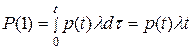Очевидно, что последний результат удовлетворяет соотношению (2.1).

Определим теперь выражение для вероятности P (k+ 1) при условии, что вероятность P (k) определяется выражением (2.1). Запишем вероятность 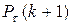сложного события, состоящего в том, что, во-первых, на интервале времени 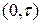произошло ровно k событий, во-вторых, на интервале времени 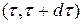(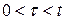) с вероятностью 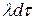произошло (k+ 1)-е событие потока и, в-третьих, на интервале 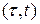события отсутствовали. Все события, составляющие рассматриваемое сложное событие, из-за отсутствия последействия независимы, поэтому получаем

.

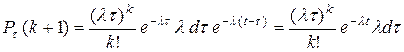Определив искомую вероятность P (k +1) путем интегрирования предыдущего выражения на интервале (0, t)

,

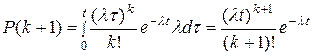подтверждаем справедливость выражения (2.1).

Теперь мы можем вернуться к рассмотрению «холодного» резервирования, упомянутого в разделе 1. При «холодном» резервировании питание на всех (n -1) резервных элементах выключено. Считается, что в таком состоянии интенсивность отказов резервных элементов практически равна нулю. В результате отказать может только единственный работающий элемент. Для простоты будем полагать, что восстановление отказавшего элемента (замена на резервный элемент) происходит мгновенно. Обозначая интенсивность отказов одного элемента через 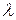и учитывая, что таких отказов может быть не более (n- 1), на основе выражения (2.1) получаем

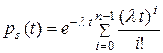. (2.2)

Пример. Продолжая пример из раздела 1, при «холодном» резервировании с учетом, что 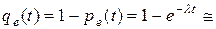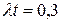, получаем

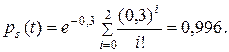
2.2. Аппроксимация потока редких событий пуассоновским потоком

Отметим интересный факт – возможность пуассоновской аппроксимации потока, образованного относительно редкими событиями, или, как еще говорят, пуассоновской аппроксимации биноминального закона распределения вероятностей. Такой прием зачастую позволяет существенно упрощать анализ происходящих процессов. Поясним это, полагая для простоты, что на интервале (0, t) рассматриваемые события могут появляться лишь в n дискретных точках. Пусть вероятность появления события в любой из этих точек одна и та же и равна p. Вероятность непоявления события в точке обозначим q= 1 -p. Тогда вероятность появления на интервале (0, t) ровно k событий определяется известной биноминальной формулой [6]

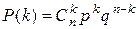, (2.3)

где .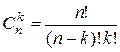

Ясно, что использовать эту формулу во многих случаях, например при редких событиях, весьма затруднительно из-за необходимости вычисления факториалов для больших чисел. Редкое событие характеризуется малым значением p. Этот факт выразим соотношением

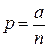, (2.4)

где 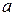– число появившихся на интервале (0, t) событий; .

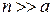Рассмотрим вероятность того, что во всех n точках рассматриваемого интервала времени событие не появится (P(0)). Вычислим ее на основе выражения (2.3)

.

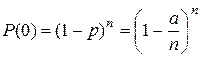Отсюда, логарифмируя и раскладывая в ряд, получаем

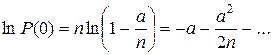
Поскольку 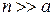, то в разложении логарифма в ряд можно ограничиться первым слагаемым. Тогда имеем

,

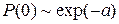где «~» обозначает предельный переход при .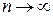

Снова обратимся к выражению (2.3) и вычислим отношение вероятностей для k и k -1 с учетом (2.4)

.

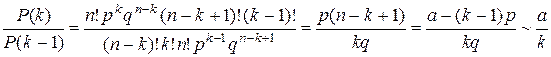В результате имеем рекуррентное соотношение

,

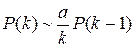из которого получаем:

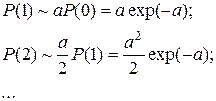
Таким образом, приходим к выражению (2.1).

2.3. Марковские модели функционирования технической системы

При оценивании надежностных характеристик технической системы удобно представлять ее функционирование в виде случайного процесса (случайной функции времени), при котором система в случайные моменты времени осуществляет переходы между своими состояниями [6]. Эти процессы с достаточной степенью приближения можно считать марковскими. Заметим, что в простейшем случае система может иметь два состояния: исправна и работает (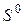), неисправна и восстанавливается (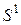). Приведем определение марковского процесса.

Случайный процесс называется марковским (процессом без последействия), если он обладает следующим свойством: для каждого момента времени 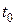вероятность любого значения процесса
в будущем (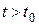) зависит только от его значения в настоящем (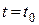) и не зависит от его значений в прошлом.

Марковские случайные процессы подразделяются на процессы с дискретными и непрерывными значениями. Если возможные значения процесса можно перечислить (перенумеровать), а сам процесс состоит в том, что время от времени он скачком переходит от одного значения к другому, то случайный процесс называется процессом с дискретными значениями. Для процессов с непрерывными значениями характерен постепенный переход от значения к значению. Примерами марковских процессов с дискретными значениями могут служить вышеупомянутые процессы функционирования системы, а марковских процессов с непрерывными значениями – случайные процессы, представляющие погрешности навигационной системы.

Среди марковских случайных процессов с дискретными значениями различают процессы с дискретным и непрерывным временем. Если переходы системы из состояния в состояние возможны только в строго определенные заранее фиксированные моменты, то процесс называют процессом с дискретным временем. Если переходы системы из состояния в состояние возможны в любой заранее неизвестный случайный момент, то процесс называют процессом с непрерывным временем или непрерывной цепью Маркова. Последние и будут применяться в дальнейшем для описания функционирования системы.

2.4. Непрерывные цепи Маркова

Пусть система может находиться в одном из N+1 дискретных состояний 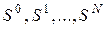и переход системы из состояния в состояние может осуществляться в любой момент времени. Обозначим через 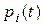вероятность того, что в момент времени t система будет находиться в состоянии 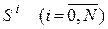. Очевидно, что для любого момента t сумма вероятностей состояний равна единице

,

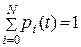так как соответствующие события несовместны и образуют полную группу.

Пусть для состояний системы предусмотрен переход из 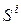в 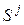и в момент времени t система находится в состоянии 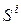. Рассмотрим промежуток времени 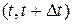, обозначив через 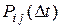вероятность того, что система, находившаяся в момент времени t в состоянии 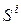, на интервале 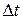перейдет из него в состояние .

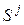Назовем интенсивностью перехода 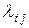предел отношения вероятности перехода системы за время 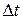из состояния 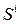в состояние 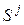к длине промежутка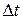

.

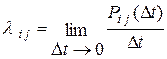Отсюда следует, что при малом 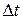имеем приближенное равенство

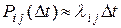. (2.5)

Если все интенсивности 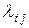не зависят от t, то марковский процесс называется однородным, в противном случае – неоднородным.

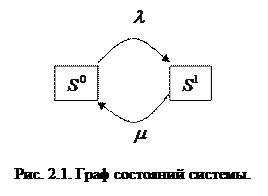Применяя аппарат непрерывных марковских цепей, при анализе надежности системы удобно пользоваться графом состояний системы, в котором вершины отражают ее возможные состояния, а дуги – направления переходов. Для простейшего случая, когда система состоит из одного восстанавливаемого элемента, имеем граф на рис. 2.1 (S ⁰ – система работает, S ¹ – система восстанавливается).

Дуги графа состояний отмечаются соответствующими интенсивностями перехода. Обычно предполагается, что не только время безотказной работы, но и время восстановления 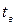элементов системы случайно и распределено по экспоненциальному закону. Так, в примере, представленном на рис. 2.1, 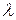– это интенсивность отказов системы, а 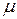– интенсивность ее восстановлений (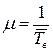, 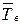– среднее время восстановления).

В заключение настоящего подраздела приведем еще одну характеристику надежности, предназначенную для безызбыточных, но восстанавливаемых систем. Эту характеристику принято называть стационарным коэффициентом готовности и обозначать 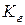. Предполагается, что в рассматриваемых системах используются средства для обнаружения отказов – средства диагностирования. Функционирование таких систем можно представить как последовательность чередующихся интервалов времени, на одном из которых система работает по прямому назначению, а на втором восстанавливается после обнаруженного отказа. При этом стационарный коэффициент готовности определяется как отношение:

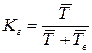. (2.6)

Ясно, что эту характеристику можно трактовать как вероятность того, что в произвольный момент времени восстанавливаемая система будет находиться в работоспособном состоянии.

Часто задачу анализа надежности описывают так, будто на систему действуют простейшие потоки отказов и восстановлений. При этом не следует забывать, что в представлении процесса возникновения аппаратурных отказов в виде потока есть известная доля условности. Действительно, после того как происходит первый отказ (первое событие потока), все равно – продолжается этот поток или прекращается. Такое представление выглядит достаточно адекватным, лишь когда восстановление системы после отказа можно считать практически мгновенным.

2.5. Резервированные системы с восстановлением.
Уравнения Колмогорова

Выше предполагалось, что отказавшие элементы системы восстановлению не подлежат. Рассмотрим теперь случай, когда производится восстановление отказавших элементов. В этом случае система при обнаружении сбоя переходит к восстановлению осуществляемого ею процесса измерения и обработки информации, а при возникновении отказа к этим действиям добавляется поиск места отказа и реконфигурация системы. Все эти операции требуют некоторого случайного времени 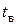восстановления. Получим для этого случая выражение для вероятности 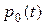безотказной работы системы как функции времени. Эта вероятность удовлетворяет дифференциальным уравнениям Колмогорова.

Для пояснения методики составления уравнений предварительно рассмотрим простой пример безызбыточной системы, состоящей из одного восстанавливаемого элемента. При этом система может находиться в одном из двух состояний: 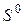– система работает, 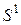– система восстанавливается, а ее поведение описывается графом состояний на рис. 2.1. Будем предполагать, что не только время безотказной работы, но и время восстановления элемента распределены по экспоненциальному закону. При этом интенсивность отказов элемента равна 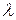, а интенсивность его восстановлений .

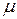Получим уравнение для вероятности 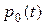того, что в момент t система будет находиться в состоянии 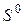. Придадим t малое приращение 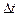и найдем вероятность 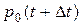того, что в момент 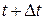система будет находиться в состоянии 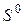. Будем предполагать, что интервал 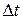настолько мал, что на нем может произойти лишь один переход. Тогда рассматриваемое событие в данном примере может произойти двумя способами:

1) в момент t система была в состоянии 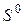и за 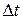не вышла из него;

2) в момент t система была в состоянии 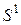и за время 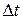перешла из него в .

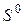Вероятность первого варианта найдем как произведение вероятности 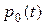того, что в момент t система была в состоянии 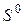, на условную вероятность того, что, будучи в состоянии 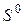, система за время 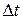не перейдет из него в состояние 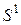. Эта условная вероятность в соответствии с (2.5) приближенно равна 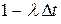. Аналогично вероятность второго варианта равна вероятности 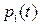того, что в момент t система была в состоянии 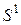, умноженной на условную вероятность перехода за время 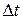в состояние : .

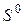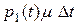Применяя правило сложения вероятностей, получаем

.

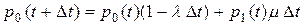Раскроем скобки в правой части, перенесем 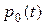в левую и разделим обе части равенства на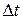

.

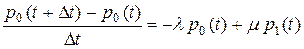Теперь устремим 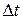к нулю и перейдем к пределу. Тогда левая часть есть не что иное, как производная функции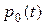

.

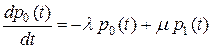Таким образом, имеем дифференциальное уравнение, которому должна удовлетворять функция 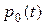. Аналогично можно получить второе уравнение

.

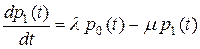Такие дифференциальные уравнения называются уравнениями Колмогорова [6]. В данном случае для описания системы достаточно одного уравнения, так как 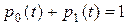. Подставляя 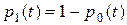в первое из уравнений, получаем

.

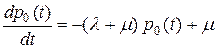Если решить это уравнение при начальных условиях 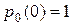, то будем иметь

.

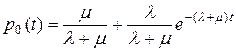Выражение для 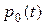определяет нестационарный коэффициент готовности, т.е. вероятность того, что в произвольный момент t система будет работоспособна. При 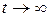в этом выражении сохраняется только постоянное слагаемое 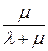, которое определяет стационарный коэффициент готовности системы.

Теперь рассмотрим простейший случай резервированной системы, состоящей из двух одинаковых элементов – основного и резервного. По-прежнему интенсивность отказов элемента будем обозначать 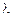, а интенсивность его восстановлений – 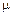. Очевидно, что система может находиться в одном из трех состояний:

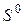– система работает;

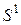– в системе работает один элемент, второй элемент отказал

и восстанавливается;

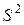– в системе отказали оба элемента, которые восстанавливаются.

Рассматриваемому случаю с очевидностью соответствует граф состояний системы на рис. 2.2.

Действуя в соответствии с методикой, использованной в предыдущем примере, получаем уравнения для вероятносте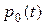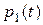й , и 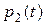состояни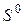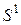й , и 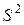соответственно:

;

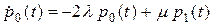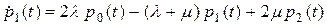; (2.7)

.

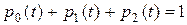Подставляя 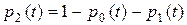во второе уравнение, получаем

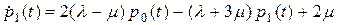. (2.8)

Выразив 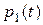из первого уравнения системы (2.7) и вычислив на основе полученного выражения 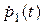, подставим 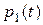и 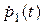в уравнение (2.8). В результате получаем линейное неоднородное дифференциальное уравнение второго порядка

.

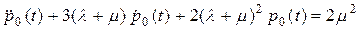Характеристический многочлен соответствующего однородного уравнения имеет вид

.

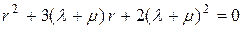Отсюда по известной формуле могут быть получены два вещественных корня 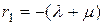и 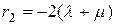, и решение однородного уравнения может быть записано как

.

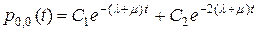Из этого решения методом вариации постоянных может быть получено частное решение неоднородного уравнения, а затем и общее

.

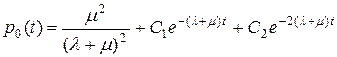Подставляя полученное выражение для 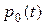и вычисляемую по нему производную 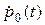в первое уравнение системы (2.7), получаем выражение для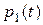

.

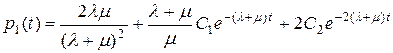Произвольные постоянные могут быть определены из начальных услови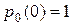й и :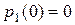

;

.

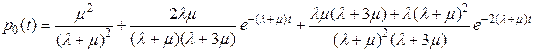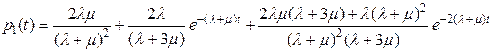Выражение для 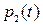определяется как разность единицы и суммы выражений для 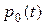и 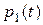. Сумма выражений для 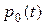и 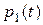определяет нестационарный коэффициент готовности, а входящие в них постоянные слагаемые – стационарный коэффициент готовности системы.

Все приведенные выражения для оценки надежности резервированных систем являются приближенными, поскольку в них не учтено влияние качества СД. При их получении неявно предполагалось, что СД идеальны и не ошибаются при оценке исправности элемента, однако на практике они могут как пропустить отказ, так и сформировать ложный сигнал об отказе.

Выше рассматривались случаи, когда избыточная система состоит из одинаковых элементов, что является частным случаем. Примером системы, для которой это условие не выполняется, может служить любая современная НС, в состав которой входит несколько различных измерителей. Эти измерители различаются по принципу действия, однако среди вырабатываемых ими параметров есть и общие, что позволяет повышать как надежность НС, так и ее точность. При этом формирование выходной информации НС происходит посредством достаточно сложного алгоритма комплексной обработки.

Вопросы

11. Мажоритарные системы.

12. Избыточные системы, использующие средства диагностирования.