2014-02-17
535
Определение 1. Выражение
,
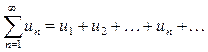где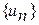 
- заданная бесконечная числовая последовательность, называется числовым рядом.
Определение 2. Конечные суммы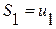 
, 
, …, 
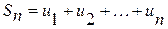называются частичными суммами ряда.
Определение 3. Если существует предел последовательности частичных сумм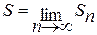 
, то ряд называется сходящимся, и число 
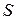называется суммой этого ряда.
Пример. Исследовать на сходимость ряд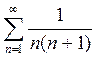 
.
Решение.
Частичная сумма этого ряда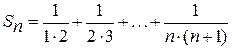 
.
Для того, чтобы вычислить предел последовательности частичных сумм, разложим общий член данного ряда на простейшие дроби
.
.
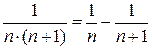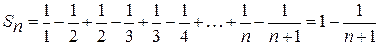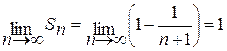. По определению данный ряд сходится и его сумма равна единице.
Пример. Исследовать на сходимость ряд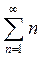 
.
Решение.
Частичная сумма этого ряда
.
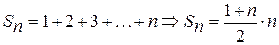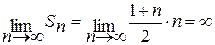, такой ряд является расходящимся.
Пример. Исследовать на сходимость ряд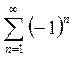 
.
Решение.
Последовательность частичных сумм: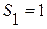 
, 
, 
, 
, …
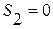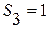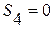Предел последовательности таких частичных сумм не существует, то есть, данный ряд расходится.
Пример. Исследовать на сходимость ряд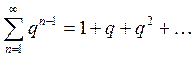 
.
Решение.
Такой ряд является геометрической прогрессией, сумма которой определяется по формуле
|
|
|
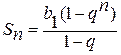, для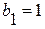 
.
.
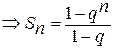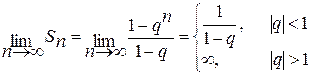Если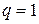 
, то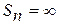 
.
Теорема 1. Отбрасывание конечного числа начальных членов ряда не влияет на его сходимость, но изменяет сумму ряда.
Доказательство.
Рассмотрим ряды 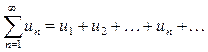(1)
и
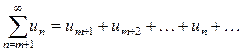(2).
Обозначим сумму отброшенных членов ряда через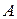 
, отбрасывает 
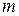членов, тогда частичная сумма для ряда (1) будет иметь вид 
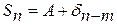, где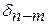 
- частичная сумма ряда (2).
При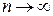 
величина 
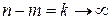, тогда 
.
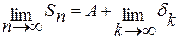Это означает, что если существует предел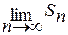 
, то будет существовать предел 
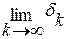. Значит, ряды (1) и (2) сходятся и расходятся одновременно.
Теорема 2. Если члены сходящегося ряда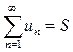 
умножить на одно и тоже постоянное число 
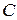, то его сходимость не нарушится, а сумма изменится в 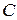раз,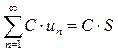 
.
Доказательство.
.
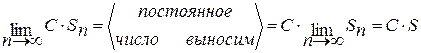Теорема 3. Два сходящихся ряда 
и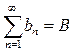 
можно почленно складывать или вычитать, при этом сходимость вновь полученного ряда сохранится и его сумма будет равна сумме или разности данных рядов, то есть 
.
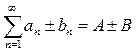Доказательство.
.
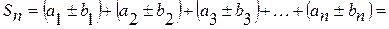
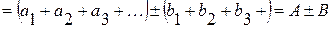Теорема 4. (критерий Коши).
Для того чтобы числовой ряд был сходящимся, необходимо и достаточно, чтобы для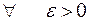 
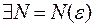, такое, что 
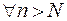и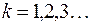 
выполнялось неравенство
.
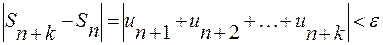Теорема 5.Необходимый признак сходимости числового ряда.
Если ряд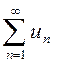 
сходится, то общий член сходящегося ряда стремится к нулю при значениях 
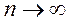, то есть
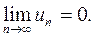
Доказательство:
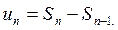Так как, по условию теоремы 1, 
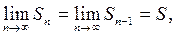то значение: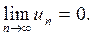 
В противном случае ряд расходится.
Это условие не является достаточным.
Покажем, что гармонический ряд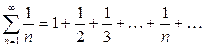 
расходится, несмотря на то, что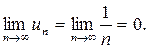 
Рассмотрим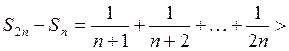 
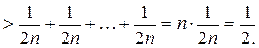
Таким образом, критерий Коши не выполняется и гармонический ряд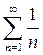 
расходится.
Примеры:
1. Исследуйте на сходимость ряд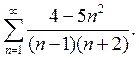 
Ряд расходится, так как для него не выполняется необходимый признак сходимости: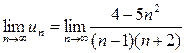 
|
|
|
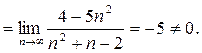
2. Исследуйте на сходимость ряд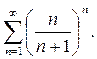 
Проверим выполнение необходимости признака сравнения:
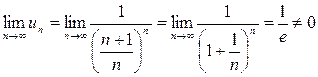ряд расходится.
