Пусть {W, F, Р } — вероятностное пространство, x 1(w), x 2(w), …, xn (w) -заданные на нем случайные величины, и A 1, A 2, …, An - конечные или бесконечные промежутки в Â 1.
Определение. Случайные величины x 1(w), x 2(w), …, xn (w) называются независимыми, если выполняется следующее равенство
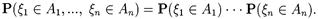 |
Как следствие, если взять в качестве Ai = (-¥, xi), i = 1,2,..., n, получим: случайные величины x 1, x 2, … xn независимы, если выполняется следующее равенство
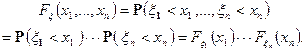
Отметим, что имеет место и обратное утверждение, т.е. если случайные величины x 1, x 2, … xn независимы, то выполняется следующее равенство
(доказательство этого утверждения можно найти в [1]).
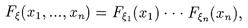 |
Для проверки независимости двух случайных величин иногда удобно пользоваться следующими результатами.
Теорема. 1). Если случайный вектор x = (x 1, x 2) имеет дискретное распределение, то случайные величины x 1 и x 2 являются независимыми тогда и только тогда, когда выполняется равенство
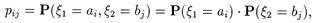 |
где ai, bj — значения случайных величин x 1 и x 2, соответственно.
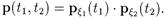 |
2) Если случайный вектор x = (x 1, x 2) имеет непрерывное распределение, то случайные величины x 1 и x 2 являются независимыми тогда и только тогда, когда выполняется равенство
|
|
|
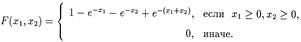 |
Пример 1. Пусть случайные величины x 1 и x 2 имеют совместную функцию распределения
Проверим, являются ли независимыми случайные величины x 1 и x 2. Найдем функции распределения этих случайных величин.
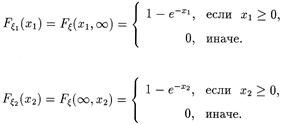 |
Теперь проверим:
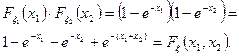
Значит, x 1 и x 2 независимые случайные величины.
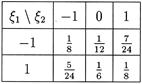
Пример 2. Пусть таблица распределения дискретного случайного вектора (x 1, x 2)следующая:
Проверим независимость случайных величин x 1 и x 2. Находим частные распределения x 1 и x 2 (см. 2.4.2.):
 |
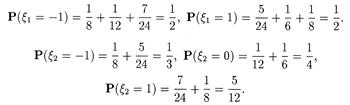
Теперь проверим соотношение из пункта 1) теоремы 1:
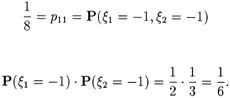 |
Соотношение 1) не выполнено. Отсюда получаем, что случайные величины x 1 и x 2 являются зависимыми.
Пример 3. Пусть x 1 и x 2 —независимые случайные величины. Рассмотрим случайную величину h = x 1+ x 2 Тогда, используя свойство 3 из предыдущего пункта и независимость случайных
величин x 1 и x 2, получаем
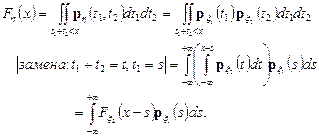
Дифференцируя последнюю формулу, получаем выражение для плотности p h(t) распределения суммы h = x 1+ x 2:
Полученное выражение носит название «формулы свертки».
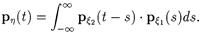 |
 2014-02-18
2014-02-18 5009
5009
