2014-02-18
759
2.8.1. Определения
Как мы помним, ярким примером класса независимых случайных величин является последовательность бернуллиевских случайных величин. Здесь же мы рассмотрим важный класс зависимых случайных величин, образующих так называемую цепь Маркова.
Пусть {W, F, Р } – некоторое вероятностное пространство, x 0, x 1, …., xn … — последовательность случайных величин со значениями в некотором множестве X.
Определение. Если при предположении
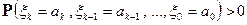
для любого k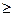 
1 выполнено условие
,
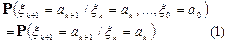то последовательность x 0, x 1, …., xn … называется цепью Маркова.
Множество X называется фазовым пространством или пространством состояний цепи.
Замечание. Если воспользоваться равенством
,
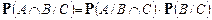то из (1) получим следующее:
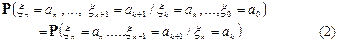
Это равенство допускает наглядную интерпретацию: если xk трактовать, например, как число клиентов в системе массового обслуживания в «настоящий» момент, (x 0, x 1, …., xk- 1) – в «прошлом», (xk+ 1, …., xn) – в «будущем», тогда соотношение (2) означает, что при фиксированных «прошлом» и «настоящем» «будущее» зависит лишь от «настоящего» и не зависит от того, каким способом система оказалась в состоянии xk, т.е. не зависит от “прошлого”. Иначе говоря, из (2) следует, что при фиксированном “настоящем” “будущее” и “прошлое” оказываются независимыми. Свойство независимости “будущего” и “прошлого” принято называть свойством Маркова, а соответствующую последовательность цепью Маркова.
|
|
|
Будем считать, что фазовое пространство X состоит из конечного или счетного множества целочисленных точек: X = {0, 1, …, N, …}. Вероятности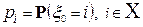 
- называют начальными вероятностями (распределение – начальным распределением), а матрицу
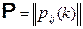, где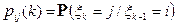 
называют матрицей переходных вероятностей в момент k (k= 1 ,…,n).
В том случае, когда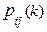 
- не зависят от k, то x 0, x 1, …., xn – называют однородной цепью Маркова. Свойства однородных цепей полностью определяются начальными вероятностями 
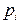и переходными вероятностями 
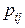. В конкретных случаях для описания эволюции цепи вместо явного выписывания матрицы используют граф (диаграмму состояний), где вершины характеризуют состояния цепи, а стрелки, идущие из одного состояния в другое – вероятности перехода.
Пример. Пусть на стоянку такси в единичные моменты времени прибывают (по одной в каждый момент) машины. Если на стоянке ожидающих клиентов нет, то машина немедленно уезжает. Обозначим через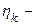 
число ожидающих клиентов, приходящих в момент k на стоянку, и предположим, что 
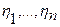- независимые случайные величины. Пусть xk – длина очереди в момент k, x 0 = 0. Тогда, если xk = i, то в следующий момент k +1 длина очереди xk+ 1 станет равной j, где
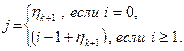
Нетрудно проверить (проверьте самостоятельно), что последовательность x 0, x 1, …., xn образуют цепь Маркова.
|
|
|
