Функция распределения (или плотность распределения) дает полную информацию о случайной величине. Однако часто бывает достаточно знать одну или несколько числовых характеристик случайной величины, которые давали бы менее полное, но более наглядное представление о случайной величине. В большинстве случаев достаточно знать некоторое «среднее» число, вокруг которого группируются все значения случайной величины (центральную тенденцию случайной величины), и ту или иную характеристику вариации значений случайной величины (степень рассеивания).
Основной наиболее употребляемой характеристикой центральной тенденции является математическое ожидание МХ случайной величины.
Определений 1. Пусть Х – дискретная случайная величина, 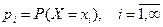 ,
, 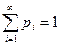 , тогда
, тогда
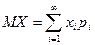 , (1)
, (1)
если ряд сходится абсолютно.
Определений 2. Пусть Х – непрерывная случайная величина, p(x) – плотность распределения, тогда
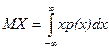 , (2)
, (2)
если интеграл сходится абсолютно.
Найдем математические ожидания случайных величин некоторых известных законов распределения.
|
|
|
1. Пусть Х имеет пуассоновское распределениес параметром l.
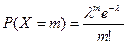 , l>0, m = 0, 1, 2,…
, l>0, m = 0, 1, 2,…
По формуле (1) имеем 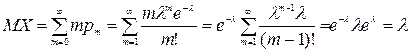 . Следовательно,
. Следовательно,
МХ = l. (3)
2. Пусть Х имеет экспоненциальное распределение с параметром l,
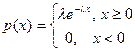 .
.
По формуле (2) имеем
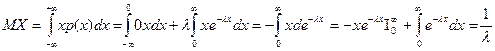 .
.
Следовательно
МХ = 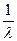 . (4)
. (4)
Пусть Х имеет равномерное распределение на интервале [ a,b ]
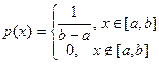 .
.
Тогда по формуле (2) имеем
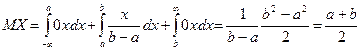
Следовательно
МХ = 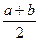 . (5)
. (5)
Определим некоторые операции над дискретными случайными величинами.
Произведением сХ случайной величины Х на постоянную величину с называется случайная величина, которая принимает значения схi с теми же вероятностями рi.
Суммой (разностью или произведением) случайных величин Х и Y называется случайная величина, которая принимает все возможные значения вида x i + yj (xi – yj xiy j) с вероятностями pij, того, что случайная величина Х примет хi, а Y – значения yj (i = 1,2, …, n; j = 1,2, …, m)
pij = P [(X = xi), (Y = yj)].
Если случайные величины X и Y независимы, т.е. независимы любые события Х = хi, Y = yj , то по теореме умножения вероятностей для независимых событий имеем
pij = P [(X = xi),(Y = yj)] = pipj.
Теорема 1. Если Y = φ (X) – функция непрерывного случайного аргумента Х, возможные значения которого принадлежат всей оси ОХ, а р (х) – плотность распределения Х, то
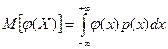 ,
,
если интеграл сходится абсолютно.
Эта теорема справедлива и для конечного отрезка возможных значений Х.
Теорема 2. Пусть Х – дискретная случайная величина принимающая значения х1, х 2, …, хn, Р (Х = хi) = pi, φ (х) – некоторая функция, тогда
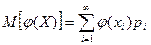 ,
,
если ряд сходится абсолютно.
 2014-02-18
2014-02-18 811
811








