Отображения

ЛЕКЦИЯ № 2

Пусть Х - некоторое числовое множество. Говорят, что на множестве Х определена функция f, если каждому числу xÎХ ставится в соответствие определенное число y=f(x). Множество Х – область определения функции, а множество Y={f(x) | xÎX} - область значений функции. Если в качестве множеств Х и Y рассматривать множества произвольной природы, а не только числовые, мы приходим к понятию отображения.

ОПРЕДЕЛЕНИЕ. Пусть А и В - два произвольных множества. Говорят, что на А определено отображение f, принимающее значения из В (f: A® B), если каждому элементу x из А ставится в соответствие _единственный. элемент y= f(x) из B.

Множество элементов xÎA, для которых определено отображение f, называется областью определения f и обозначается d_f.

Если имеется какой-либо элемент хÎА, то соответствующий ему элемент yÎB будем называть образом x. Пусть C - некоторое подмножество множества A, образом множества C называется множество вида {f(x) | xÎC}. Образ области определения называется областью значений отображения f и обозначается r_f (т.е. r_f =f(d_f)=f(X)).

Если задать yÎВ, то множество соответствующих ему x, т.е. таких, что y = f(x) будем называть прообразом y и обозначать f^-1(y), f^-1(y)={xÎX | y = f(x)}. В общем случае обратное отображение f^-1 неоднозначно.

Отображение i: A ® A такое, что i(x)=x для любого xÎA называется тождественным отображением.

Пусть f: A ® B и g: B ® C. Отображение h: A ® C, такое, что каждому элементу xÎA ставится в соответствие единственный элемент h(x) = g(f(x)), называется композицией (или суперпозицией) отображений f и g и обозначается g o f.

Отображение f: А ® В называется сюръекцией А на В, если множество образов всех элементов из А совпадают с множеством В. Это обозначается как f(А) = В. Другое эквивалентное определение сюръекции - это отображение, при котором каждый элемент из В имеет прообраз в множестве А.

Если для любых x₁, x₂ÎA таких, что x₁¹x₂, получается, что f(x₁)¹f(x₂), т.е. разным элементам соответствуют различные образы, то это отображение f называется инъекцией.

Отображение f, которое является одновременно сюръекцией и инъекцией, называется биекцией, или взаимно однозначным отображением.

Если между А и В установлено биективное отображение, то говорят, что множества А и В эквивалентны. Эквивалентность множеств обозначается A~B.

Основные свойства отображений можно сформулировать в виде следующих теорем.

ТЕОРЕМА 1. f ^-1(AÈB) = f ^-1(A)Èf ^-1(B) - прообраз объединения двух множеств равен объединению их прообразов.

ДОКАЗАТЕЛЬСТВО. Пусть xÎf ^-1(A)Èf ^-1(B). Тогда или xÎf ^-1(A) или хÎf ^-1(B). В первом случае y=f(x)ÎА, во втором yÎВ. В любом случае yÎАÈВ, поэтому xÎf^-1(AÈB).

Докажем обратное включение. Пусть xÎf ^-1(AÈB), тогда y=f(x)ÎAÈB. Значит или yÎА, или yÎВ. Если yÎА, то f ^-1(y) Í Íf ^-1(A). Так как xÎf ^-1(y), то отсюда следует, что xÎf ^-1(A). Если же yÎВ, то f ^-1(y)Íf ^-1(B), что влечет xÎf ^-1(В). В любом случае xÎf ^-1(A)Èf ^-1(B). Поэтому, если xÎf ^-1(AÈB), то xÎf ^-1(A)Èf ^–1(B), что и требовалось доказать.

ТЕОРЕМА 2. f ^-1(AÇB)=f ^-1(A)Çf ^-1(B) - прообраз пересечения двух множеств равен пересечению их прообразов.

ДОКАЗАТЕЛЬСТВО. Пусть xÎf ^-1(AÇB), тогда y=f(x)ÎAÇB. Значит, yÎА и yÎВ. Если yÎА, то f ^-1(y)Íf ^-1(A), а если yÎВ, то f ^-1(y)Íf ^-1(B). Эти включения должны выполняться одновременно, следовательно, f ^-1(y)Íf ^-1(A)Çf ^-1(B), а значит, хÎf ^-1(A)Çf ^-1(B). Таким образом, f ^-1(AÇB)Íf ^-1(A)Çf ^-1(B).

Докажем обратное включение. Пусть xÎf ^-1(A)Çf ^-1(B), тогда xÎf ^-1(A) и xÎf ^-1(B). Если xÎf ^-1(A), то y=f(x)ÎA. Если же xÎf ^-1(B), то y=f(x)ÎB. Так как yÎA и yÎB, то yÎAÇB и поэтому f ^-1(y) Í f ^-1(AÇB). Значит, хÎf ^-1(AÇB) и отсюда следует, что f ^-1(A)Çf ^-1(B) Í f ^-1(AÇB).

Эти два включения означают, что f ^-1(AÇB)=f ^-1(A)Çf ^-1(B), что и требовалось доказать.

ТЕОРЕМА 3. Образ объединения двух множеств равен объединению их образов.

ДОКАЗАТЕЛЬСТВО. Пусть yÎf(AÈB), тогда для любого x из множества f ^-1(y) выполняется принадлежность хÎAÈB. Поэтому xÎA или xÎB. В первом случае y=f(x)Îf(A), во втором случае y=f(x)Îf(B). Так как yÎf(A) или yÎf(B), то yÎf(A)Èf(B) и, следовательно, f(AÈB)Íf(A)Èf(B).

Докажем обратное включение. Пусть yÎf(A)Èf(B), тогда yÎf(A) и f ^-1(y)ÍA или yÎf(B) и f ^-1(y)ÍB. Соответственно получаем, что xÎA или xÎB, т.е. xÎAÈB и тогда y=f(x)Î Îf(AÈB). Доказано включение f(A)Èf(B)Íf(AÈB). Следовательно, f(AÈB)=f(A)Èf(B).

ЗАМЕЧАНИЕ. Образ пересечения двух множеств не обязательно совпадает с пересечением их образов. Рассмотрим пример.

Пусть A и B - множества точек на плоскости:

A = { (x, y) | 0 £ x £ 1, y=2 },

B = { (x, y) | 0 £ x £ 1, y=1 }.

С помощью проектирования точек на ось ОХ построим отображение А и В на множество С = { (x, y) | 0 £ x £ 1, y=0 }. Так как f(A) = C, f(B) = C, то f(A)Çf(B) = C. Но множества A и B не пересекаются и f(AÇB)=f(Æ)=Æ, т.е. мы показали, что f(AÇB)¹ ¹f(A)Çf(B).

Теоремы 1, 2, 3 остаются в силе при любом конечном и бесконечном числе множеств. Например, теорема 1 примет вид:

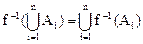
где A₁, A₂,... - некоторая система множеств.

Докажем (1) с помощью метода математической индукции.

1. При n=2 равенство f ^-1(A₁ÈA₂)=f ^-1(A₁)Èf ^-1(A₂) справедливо согласно доказанной теореме 1.

2. Предположим, что равенство верно при любом n £ k.

3. Докажем, что равенство верно при n = k+1.

Обозначим

B = .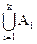

Тогда

f ^-1(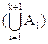)=f ^-1(BÈA_k+1)= f ^-1(B)Èf ^-1(A_k+1),

так как для двух множеств В и A_k+1 теорема верна. Но по предположению индукции для k множеств теорема также верна, поэтому

f ^-1(B)=.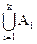

Отсюда следует требуемое равенство.

Множества, между которыми можно установить биективное отображение называются эквивалентными.

Легко видеть, что эквивалентность множеств обладает свойством транзитивности, т.е. если A~B и B~C, то A~C. Признаки эквивалентности множеств дают следующие

ТЕОРЕМЫ Кантора-Бернштейна.

1. Если AÍBÍC, причем A~C, то A~B.

2. Если A эквивалентно подмножеству множества B, а B эквивалентно подмножеству множества A, то A~B.