Теорема Гаусса-Маркова

Предположим, что:

1) Y = Xb + e;

2) X – детерминированная матрица размерности nхk, имеющая максимальный ранг k;

3) E(e) = 0; V(e) = E(ee`) = s²In.

Тогда оценка метода наименьших квадратов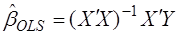

является наиболее эффективной (в смысле наименьшей дисперсии) оценкой в классе линейных несмещенных оценок.

Доказательство. Обозначим .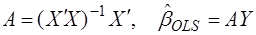

Любую другую линейную оценку b можно без ограничения общности представить в виде b = (A + C)Y, где C - некоторая матрица размерности nхk.

1. Покажем, что МНК-оценка (см. уравнение (46)) является несмещенной оценкой b:

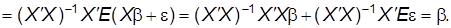(49)

Из условия несмещенности оценки b получаем, что для всех b справедливо соотношение

b = Eb = (A + C)EY = (A + C)Xb = (I + CX)b,

откуда следует, что CX = 0.

2. Подсчитаем матрицу ковариаций МНК-оценки:

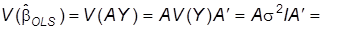
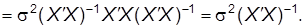(50)

(Здесь мы использовали симметричность матрицы X`X).

3. Используя полученное выше равенство CX = 0, получаем

b - b = (A + C)Y - b = (A + C)Xb + (A + C)e - b = AXb - b + CXb +

+ (A + C)e = (A + C)e, так как CX = 0 и AX = 1.

Вычислим теперь матрицу ковариаций вектора b:

V(b) = E((b - b)(b - b)`) = E((A +C)ee`(A + C)`) = (A + C)s<sup>2</sup>I (A + C)`=

= s² [AA` + CA` + AC` + CC`] = s² [(X`X)<sup>-1</sup> X`X (X`X)^-1 +

+ CX (X`X)<sup>-1</sup> + (X`X)^-1 X`C` + CC`] = s<sup>2</sup>(X`X)^-1 + s²CC`.

Таким образом (см. формулу (50)),

V(b) = V(b_ols) + s²CC`.

Матрица CC` неотрицательно определена, поэтому

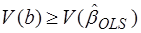. (51)

Отсюда следует утверждение теоремы. В самом деле, i-й диагональный элемент матрицы V(b) равен дисперсии i-й компоненты вектора коэффициентов V(b_i). Поэтому из (51) следует соответствующее неравенство для дисперсий оценок коэффициентов регрессии

,

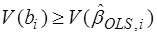что и требовалось доказать.